Controlling human causal inference through in silico task design - methods
인과 관계를 학습하는 능력은 생존에 필수적이다. 인간의 두뇌는 높은 기능적 유연성을 지니고 있어 효과적인 인과 추론(causal inference)이 가능하며, 이는 다양한 학습 과정의 근간을 이룬다. 기존 연구들은 환경적 요인이 인과 추론에 미치는 영향에 초점을 맞추어왔지만, 본 연구에서는 근본적인 질문을 제기한다: 이러한 환경적 요인을 전략적으로 조작하여 인과 추론을 통제할 수 있을까?
이 논문은 “과제 제어(task control) 프레임워크” 를 제안하여 인간의 인과 학습을 조율하는 방법을 연구한다. 연구진은 2인 게임(two-player game) 구조 를 활용하여, 신경망(neural network)이 인간 인과 추론 모델과 상호작용하면서 실험 과제의 변수를 조작하는 방식을 학습하도록 설계하였다. 구체적으로, 태스크 컨트롤러(task controller) 가 실험 디자인을 최적화하면서 인과 구조의 복잡성을 반영할 수 있는지를 검증하였다. 126명의 인간 참가자를 대상으로 한 실험 결과, 태스크 컨트롤을 통해 인과 추론의 성과 및 학습 효율을 조정할 수 있음이 확인되었다. 특히, 태스크 컨트롤 정책은 인간의 인과 추론 과정에서 나타나는 “원샷 학습(one-shot learning)” 의 특성을 반영하는 것으로 나타났다. 이러한 연구 프레임워크는 인간 행동을 특정 방향으로 유도할 수 있는 응용 가능성을 제시 하며, 향후 교육, 치료, 그리고 인공지능을 활용한 학습 최적화 등의 분야에서 중요한 역할을 할 것으로 기대된다.
Introduction
인과 추론(causal inference)은 관찰을 통해 원인과 결과의 관계를 학습하는 능력을 의미하며, 이는 강화 학습(reinforcement learning, RL)과 의사결정 과정에서 핵심적인 역할을 한다. 기존 연구에서는 동물 실험을 통해 최소한 두 가지 다른 방식의 인과 학습 패턴이 존재한다는 사실이 밝혀졌다. 첫 번째는 점진적 학습(incremental inference)으로, 충분한 경험을 쌓은 후 점진적으로 결과를 예측하는 방식이다. 반면, 두 번째는 원샷 학습(one-shot inference)으로, 단 한 번의 경험을 통해 강력한 신념을 형성하는 방식이다. 이러한 행동 패턴은 동물뿐만 아니라 인간에게도 동일하게 나타나며, 최신 연구에서는 인간의 뇌가 두 가지 학습 방식을 유연하게 조절할 수 있다는 신경학적 근거가 발견되었다. 이는 인간이 환경 속에서 복잡한 원인-결과 관계를 동적으로 해결하며 새로운 과제를 학습할 수 있음을 의미한다.
이전 연구들은 인간의 인과 추론이 환경적 요인에 의해 영향을 받는다는 점을 분석하는 데 집중해왔다. 예를 들어, 사람들이 새로운 과제를 학습할 때, 환경이 불확실성이 높은 경우에는 신뢰할 수 있는 성과를 보장하기 위해 점진적 학습을 선호하는 경향이 있다. 반면, 불확실성이 적은 환경에서는 보다 신속하고 효율적인 원샷 학습을 활용하는 것이 최적의 전략이 될 수 있다. 이러한 연구들은 인간의 인과 추론이 단일한 방식이 아니라 환경적 맥락에 따라 유연하게 조정된다는 사실을 보여준다.
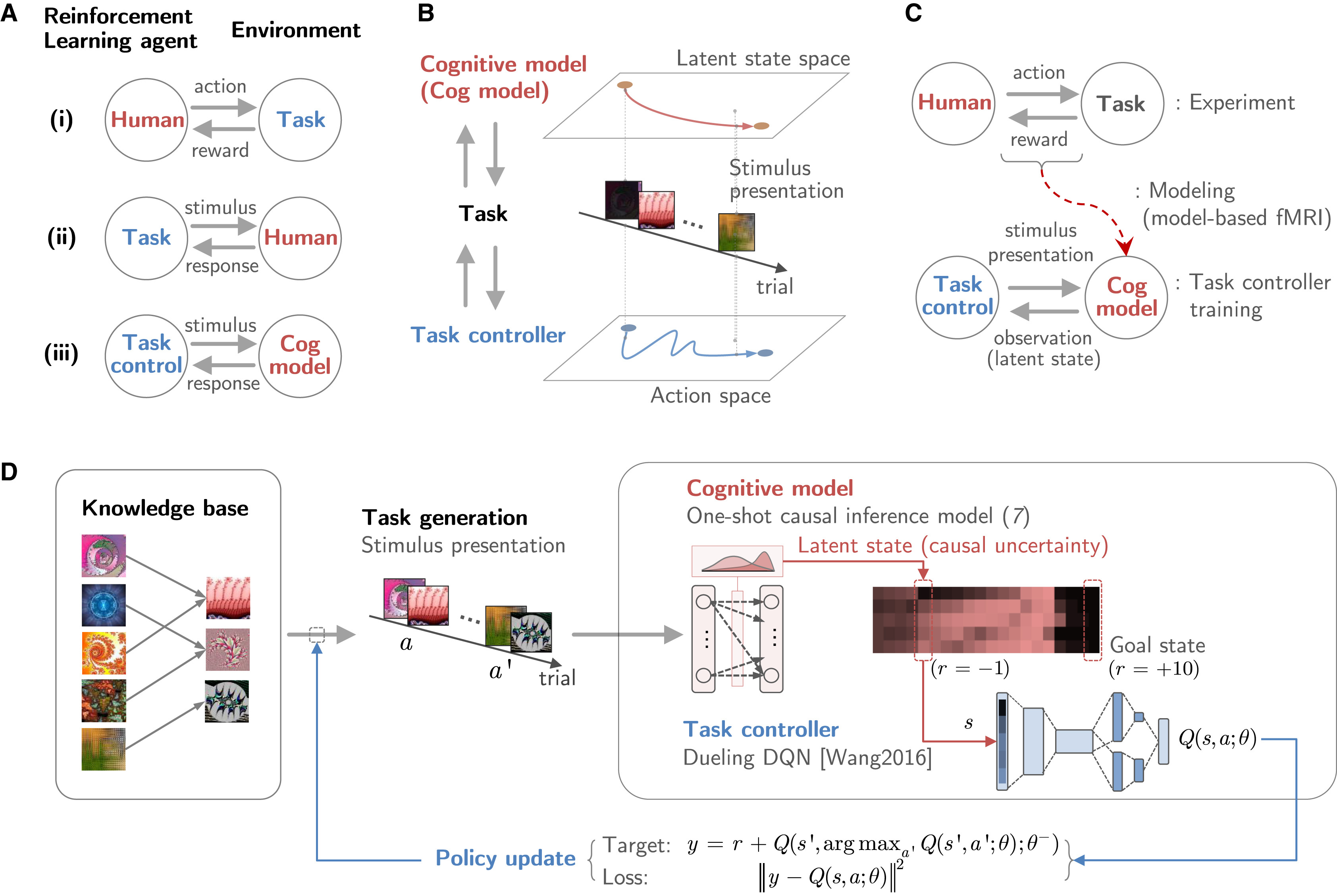
이러한 맥락에서 연구진은 인간의 인과 추론 과정이 환경적 요인에 의해 자연스럽게 조정되는 것이 아니라, 전략적으로 조작될 수 있는지에 대한 근본적인 질문을 던진다. 즉, 인간의 인지 과정을 특정 방향으로 유도할 수 있는지가 핵심적인 연구 질문이다. 이를 탐구하기 위해 연구진은 “태스크 컨트롤(task control)”이라는 개념을 제안하였다. 태스크 컨트롤은 인간의 인과 학습 과제를 설계하고 조율하는 프레임워크로, 딥러닝 기반의 태스크 컨트롤러(deep-RL-based task controller)를 활용하여 인간의 인과 추론 모델과 상호작용하면서 학습 변수를 조작하는 방식으로 설계되었다. 이 태스크 컨트롤러는 인간의 인과 추론 모델이 학습하는 과정을 탐색하고, 실험 변수를 조작하여 인간의 학습 성과와 효율성을 변화시키는 방식을 학습한다.
연구진은 태스크 컨트롤이 인간의 인과 추론을 조절할 수 있는지를 검증하기 위해, 세 가지 태스크 컨트롤 조건을 설정하여 실험을 진행하였다. 첫 번째 조건인 Bayesian+는 점진적 학습 방식을 촉진하여 충분한 학습 시간이 주어졌을 때 신뢰성 높은 성과를 보장하는 것을 목표로 한다. 두 번째 조건인 Oneshot+는 신속한 학습을 유도하여 짧은 시간 내에 높은 학습 효율을 달성하는 것을 목적으로 한다. 마지막으로 Oneshot– 조건은 학습을 어렵게 만들어 인과 추론을 방해하며, 이를 통해 동기 부여, 트라우마 억제, 나쁜 습관 제거 및 심리적 회복력 증진과 같은 응용 가능성을 탐색하는 데 초점을 맞춘다.
126명의 인간 참가자를 대상으로 한 실험 결과, 태스크 컨트롤을 통해 인과 추론의 성과 및 학습 효율을 조정할 수 있음이 실증적으로 확인되었다. 특히, 태스크 컨트롤의 효과는 개별 참가자의 학습 특성을 반영한 인지 모델을 사용할 때 더욱 극대화되는 것으로 나타났다. 이는 태스크 컨트롤이 단순히 실험 디자인을 최적화하는 것이 아니라, 인간 인과 추론의 본질적인 특성을 반영하는 방식으로 작동한다는 점을 시사한다.
Methods
연구진은 인간의 인과 추론 학습 과정에서 태스크 컨트롤이 어떻게 작용하는지를 분석하기 위해, 126명의 성인 참가자를 모집하여 실험을 수행했다. 총 126명(남녀 포함, 연령 18~56세) 참가 참가자들은 사전에 정신적·신경학적 장애가 없는지 확인, 모든 참가자는 실험 전에 서면 동의(Informed Consent)를 받았으며 세 가지 태스크 컨트롤 조건(Bayesian+, Oneshot+, Oneshot–) 중 하나에 무작위로 배정되었다.
Task control: In silico task design for guiding human causal inference
이 연구에서 제안하는 태스크 컨트롤(Task Control) 프레임워크 는 인간의 인과 추론 과정을 조정하기 위한 컴퓨터 기반 실험 설계(in silico task design) 방식이다. 기존의 과제 학습(task learning)에서는 학습자가 환경과 상호작용하며 인과 관계를 학습하지만, 본 연구에서는 이를 역으로 조작하여 과제가 인간의 인지 모델을 조정하도록 설계 한다. 즉, 태스크 컨트롤러(task controller) 가 인간의 인과 추론 모델과 상호작용하며 실험 변수를 조정함으로써 특정한 학습 경로를 유도하는 방식이다.
1. 마르코프 결정 과정(MDP) 정의
태스크 컨트롤러 문제는 5-튜플 \((U, A, T, R, \gamma)\) 로 구성된 MDP로 모델링된다.
\(U\): 상태 공간 (State space) \(A\): 행동 공간 (Action space) \(T\): 전이 함수 (Transition function) \(R\): 보상 함수 (Reward function) \(\gamma\): 할인 계수 (Discount factor)
2. MDP 구성 요소 설명
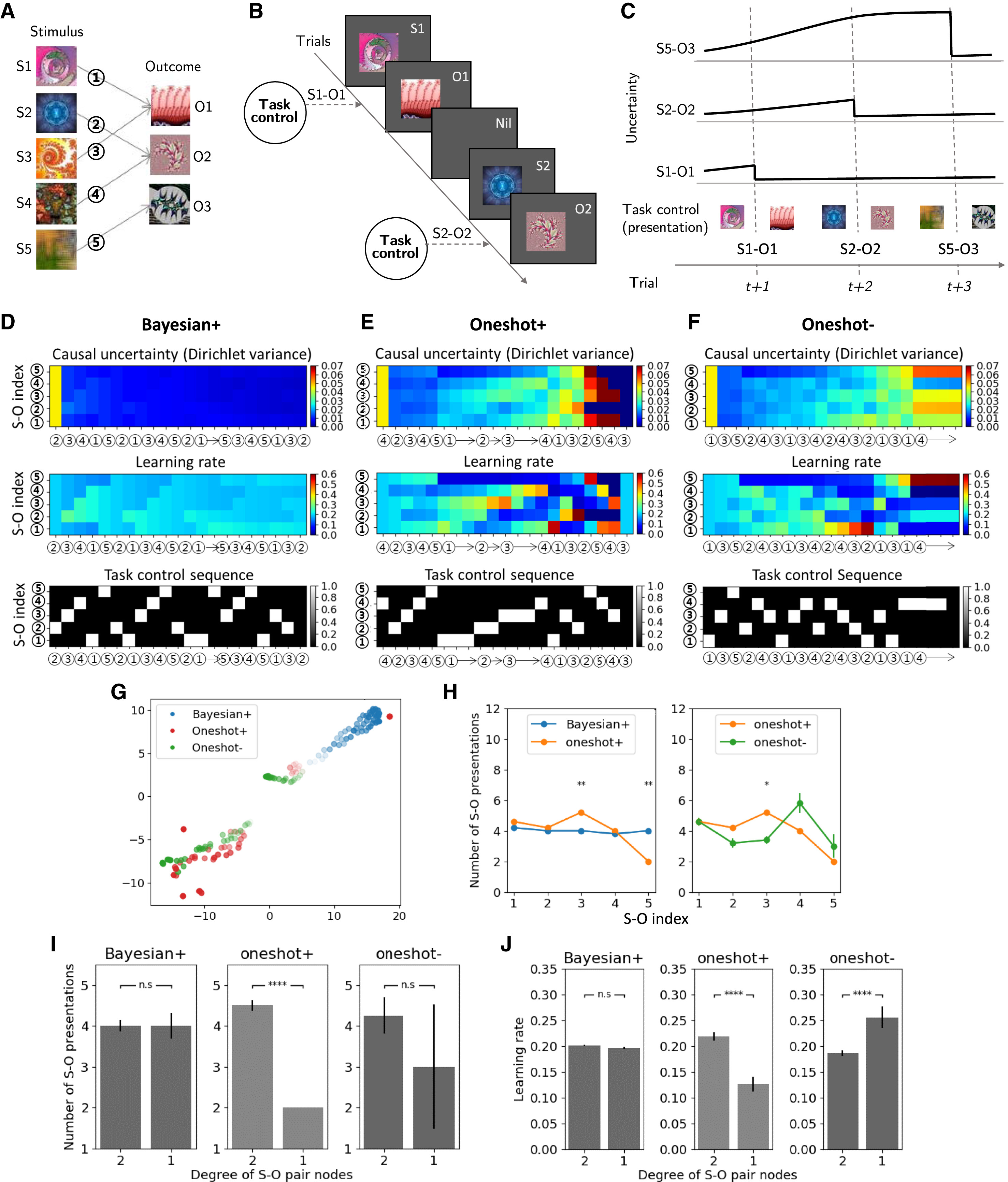
태스크 컨트롤러의 상태 \(u_i\) 는 특정 시점 \(i\) 에서 각 S-O 페어(Stimulus-Outcome Pair)의 인과적 불확실성(causal uncertainty) 을 포함하는 벡터로 정의된다. \(u_i = \{ u_1, u_2, ..., u_N \} \in U\)
\(u_k\) 는 특정 S-O 페어 \(p_k\) 의 인과적 불확실성이며, 인과적 불확실성 \(u_k\) 는 학습자가 해당 S-O 관계를 얼마나 신뢰하는지에 대한 불확실성을 나타낸다. 연구에서는 베이지안 인과 추론 모델(Bayesian Inference Model) 또는 원샷 학습 모델(One-shot Learning Model) 을 사용하여 이를 정량화했하였다. 태스크 컨트롤러의 목표 상태(goal state) \(u_{\text{goal}}\) 은 모든 S-O 관계의 인과적 불확실성이 특정 임계값 이하로 낮아진 상태이다.
\[u_{\text{goal}} = \{ u_1, u_2, ..., u_N \}, \quad \text{where } u_k \leq u_{\text{TH}}, \forall k\]즉, 태스크 컨트롤러는 인간 학습자가 가능한 한 빨리 인과적 불확실성을 줄일 수 있도록 실험 조건을 조정하는 역할을 한다.
태스크 컨트롤러가 특정 상태 \(u_i\) 에서 행동 \(a_i\) 를 선택하면, 인간 인지 모델이 다음 상태 \(u_{i+1}\) 로 전이되며, 전이 확률 \(P(u_i, a_i, u_{i+1})\) 는 인지 모델 M에 의해 결정되는 함수 로 표현된다.
\[T: U \times A \times U \rightarrow [0, 1] P(u_i, a_i, u_{i+1}) = M(u_i, a_i, u_{i+1})\]여기서 \(M\) 은 인간의 인과 학습 과정을 설명하는 인지 모델이며 어떤 자극-결과 페어를 보여주었을 때, 인간 학습자가 해당 관계를 학습하는 정도를 반영한다. 또한 태스크 컨트롤러는 인간 인지 모델이 목표 상태(goal state)에 도달하도록 유도 해야하기 때문에 이를 위해 보상 함수 \(R\) 을 다음과 같이 정의한다. 목표 상태 \(u_{\text{goal}}\) 에 도달하면 +1의 보상 을 부여하고, 그렇지 않으면 -1의 보상 을 부여한다.
\[R: U \times A \times R \rightarrow R\] \[R(U) = \begin{cases} 1, & \text{if } u_U \leq u_{\text{TH}} \\ -1, & \text{otherwise} \end{cases}\]3. 태스크 컨트롤러의 학습 과정
태스크 컨트롤러의 학습 목표는 기대 보상(expected return)을 최대화하는 최적 정책 \(\pi^*\) 을 찾는 것이다. \(V^{\pi}(u)\) 는 특정 상태 \(u\) 에서 정책 \(\pi\) 를 따를 때 기대되는 총 보상 값이다.
\[V^{\pi}(u) = \mathbb{E}_{\pi} \left[ \sum_{i=0}^{M-1} \gamma^i R_{i+1} | u_0 = u, \pi \right]\]또한 태스크 컨트롤러는 Dueling DDQN 구조를 활용하여 학습 성능을 개선하였다. \(Q(s, a)\) 는 현재 상태에서 행동 \(a\) 를 선택했을 때의 기대 보상을 나타낸다.
\[Y^{DDQN}_t = R_{t+1} + \gamma Q(s_{t+1}, \arg\max_a Q(s_{t+1}, a; \theta); \theta^-)\]Key concepts
1. 인과적 불확실성 (Causal Uncertainty)
주어진 자극(S, Stimulus) 과 결과(O, Outcome) 사이의 인과 관계는 확률 분포 로 정의된다. 이때, 확률 분포의 평균(mean)은 인과 강도(causal strength) 를 나타내고, 분산(variance)은 인과적 불확실성(causal uncertainty) 을 의미한다. 이 실험에서 인과적 불확실성은 특정 S-O 관계의 강도에 대한 불확실성 수준을 나타내게 된다. 인과적 불확실성 값이 크면, 해당 관계에 대한 신뢰도가 낮고 학습이 필요한 상태를 의미한다. 연구에서는 인간 인과 추론 모델(cognitive model of human causal inference) 을 활용하여 태스크 컨트롤러 학습 과정에서 인과적 불확실성을 추정하도록 한다.
2. 인과적 복잡성 (Causal Complexity)
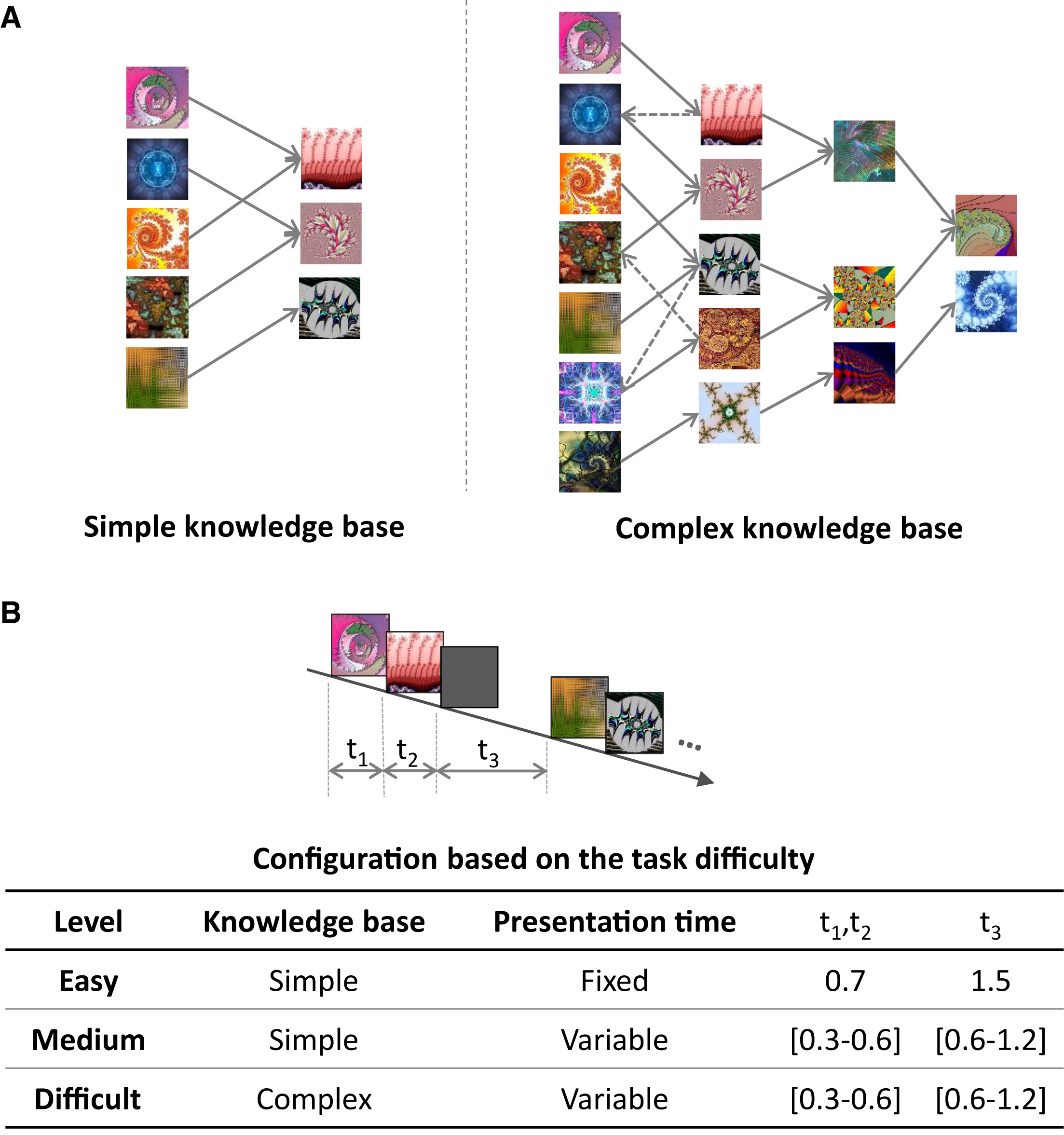
인과적 복잡성은 하나의 지식 베이스(Knowledge Base, KB) 내에서 존재하는 S-O 관계의 수 를 의미한다. 인과적 복잡성이 높을수록, 더 많은 인과적 연관 관계(그래프 내의 간선 수)가 존재한다. 복잡한 환경에서는 학습자가 더 많은 S-O 페어를 탐색하고 학습해야 하므로 학습 난이도가 증가한다. 예를 들어 단순한 경우(Simple case)는 5개의 S-O 관계 (Figure 3B-left), 복잡한 경우(Complex case)는 17개의 S-O 관계 (Figure 3A-right)를 사용한다.
Task control problem
태스크 컨트롤러는 기대 보상(expected return)을 최대화하는 방향으로 학습된다. 이를 위해, 다음과 같은 강화 학습 목표를 설정한다.
\[V^{\pi}(u) = \mathbb{E}_{\pi} \left[ \sum_{i=0}^{M-1} \gamma^i R_{i+1} | u_0 = u, \pi \right]\]\(V^{\pi}(u)\) 는 특정 상태 \(u\) 에서 정책 \(\pi\) 를 따를 때 기대되는 총 보상 값이다. \(\gamma\) 는 할인 계수(discount factor)로, 미래 보상의 중요도를 조절하는 값이 된다. 즉, 태스크 컨트롤러는 학습자가 빠르고 효과적으로 인과적 불확실성을 줄이도록 유도하는 방식으로 학습된다. 상술하였듯이 태스크 컨트롤러의 상태 \(u\) 는 각 S-O 페어의 인과적 불확실성 값으로 표현되는데, 초기 상태는 학습자의 초기 인과적 불확실성 수준 에 의해 결정된다. 실험에서, 태스크 컨트롤러는 각 단계에서 학습자가 어떤 S-O 페어를 학습해야 하는지를 결정하는 역할을 한다. 결국 태스크 컨트롤러는 각 단계에서 학습자의 상태 \(u\) 를 분석하고, 최적의 행동 \(a\) 를 선택하여 보상을 최대화하는 방향으로 학습된다.
Computational Model of Causal Human Inference
1. 인과 학습 모델의 유형
1. 베이지안 인과 추론 모델 (Bayesian Inference Model)
인간이 점진적으로(Step-by-Step) S-O 관계를 학습 한다는 가설을 기반으로 한다. 동일한 S-O 페어를 반복적으로 경험할수록 인과적 불확실성(\(u\))이 감소 하며, 학습이 이루어진다. 태스크 컨트롤러 Bayesian+ 는 이 모델을 기반으로 학습자를 점진적 학습 패턴으로 유도한다.
\[\text{If } p_k \text{ is observed multiple times, then } u_k \to 0\]즉, S-O 관계를 반복적으로 노출하면 학습자가 점진적으로 인과 관계를 신뢰하게 된다. 이는 Bayesian+ 컨트롤러의 원리 이며, 태스크 컨트롤러는 학습자가 점진적으로 불확실성을 줄이도록 최적의 실험 설계를 학습 한다.
2. 원샷 인과 학습 모델 (One-shot Causal Learning Model)
인간이 한 번의 경험만으로도 강한 인과적 신념을 형성할 수 있다 는 가설을 기반으로 한다. 베이지안 모델과 달리, 학습률(learning rate)이 동적으로 변하며, 인과적 불확실성에 따라 조정된다. 태스크 컨트롤러 Oneshot+ 및 Oneshot- 는 이 모델을 활용하여 원샷 학습을 촉진하거나 억제할 수 있다.
\[\text{If } p_k \text{ is observed once, then } u_k \approx 0\]즉, Oneshot+ 컨트롤러는 특정 S-O 페어를 한 번만 경험해도 신뢰하도록 학습을 유도 한다. 반면, Oneshot- 컨트롤러는 원샷 학습 효과를 최소화하고, 점진적 학습을 유도 한다.
2. 인과 학습 모델의 수학적 표현
1. 잠재 클래스 모델
인간의 인과 추론을 모델링하기 위해 잠재 클래스 모델(Latent Class Model)을 적용 한다. 이 모델은 S-O 관계의 확률을 다음과 같이 정의한다.
\[P(O | q) = \begin{cases} q_1, & \text{if } O = S_1 \\ q_2, & \text{if } O = S_2 \\ q_3, & \text{if } O = S_3 \end{cases}\]\(q_i\) 는 \(S_i\) 가 결과 \(O\) 를 유발할 확률을 나타내며, 확률 값 \(q\) 는 디리클레 분포(Dirichlet Distribution) 를 따른다.
\[(q_1, q_2, q_3) \sim Dir(\lambda_1, \lambda_2, \lambda_3)\]사전 확률(prior)은 균등 분포(uniform)로 설정되며, 특정 S-O 페어 \(p\) 가 여러 번 제시되면, 사후 확률(posterior probability)이 업데이트된다.
2. 베이지안 인과 추론 모델 (Bayesian Inference Model)
베이지안 모델은 모든 S-O 페어가 동일한 학습 효과를 갖도록 가정 한다. 학습률 \(g_i\) 는 고정된 상수(\(C\)) 로 설정되며, 학습 과정에서 변하지 않는다. 즉, 특정 S-O 페어가 반복될수록 학습자가 해당 관계를 더 강하게 신뢰하게 된다.
\[\Delta a_i = g_i x_i, \quad \text{where } g_i = C\] \[E(q_i | E) = \frac{a_i}{a_0}\] \[Var(q_i | E) = \frac{a_i (a_0 - a_i)}{a_0^2 (a_0 + 1)}\]평균 \(E(q_i \mid E)\)는 인과적 강도를 나타내며, 반복 노출될수록 값이 증가 한다. 반대로 분산 \(Var(q_i \mid E)\)는 인과적 불확실성을 나타내며, 반복 노출될수록 값이 감소 한다.
3. 원샷 인과 학습 모델 (One-shot Causal Learning Model)
원샷 모델은 학습률이 동적으로 조정 된다. 특정 S-O 페어의 불확실성이 크면, 해당 페어의 학습률이 증가하고, 반대로 불확실성이 낮으면 학습률이 감소한다.
\[g_i = \frac{\exp(t \cdot Var(q_i | E))}{\sum_j \exp(t \cdot Var(q_j | E))}\]위 식에서 \(t\) 는 온도(temperature) 파라미터로, 학습률의 변화를 조정하는 역할을 한다. 결과적으로, 불확실성이 높은 S-O 페어일수록 더 빠르게 학습 된다.
\[\text{If } Var(q_i | E) \text{ is high, then } g_i \text{ is large.}\]즉, Oneshot+ 컨트롤러는 특정 S-O 관계가 한 번만 제시되더라도 강한 신뢰를 형성하도록 유도 한다. 반면, Oneshot- 컨트롤러는 원샷 학습을 억제하고 점진적 학습을 유도하는 방식으로 작동한다. 이 컨트롤러는 학습자가 여러 번 반복적인 경험을 통해서만 인과 관계를 학습할 수 있도록 학습률을 낮추는 방향으로 실험을 조정한다. 이를 통해 학습자는 특정 S-O 관계를 여러 번 경험해야만 신뢰를 형성할 수 있으며, 인과적 불확실성이 점진적으로 감소하도록 설계된다.
태스크 컨트롤러의 강화 학습 과정
태스크 컨트롤러의 학습 과정은 강화 학습 기반의 반복적인 상호작용 을 통해 이루어진다. 이 과정에서 태스크 컨트롤러는 인간 인지 모델(cognitive model)과 반복적으로 상호작용하며 최적의 정책을 학습 한다. 연구진은 이러한 상호작용을 이중 플레이어 확률 게임(Two-player Stochastic Game) 으로 모델링하였다. 이는 마르코프 결정 과정(MDP, Markov Decision Process) 및 반복 게임(Repeated Games)을 확장한 개념으로, 태스크 컨트롤러와 인간 인지 모델이 서로 적응하며 학습하는 구조를 반영 한다.
1. 확률 게임(Stochastic Game) 모델링
태스크 컨트롤러의 학습은 6-튜플(6-Tuple) 확률 게임 으로 정의된다.
\[(U, N, A, T, r, \gamma)\]이 게임에서는 태스크 컨트롤러와 인간 인지 모델이 상호작용하면서 학습이 진행 된다. 각 플레이어(태스크 컨트롤러, 인간 인지 모델)는 자신의 전략을 조정하며 최적의 학습 조건을 찾아가는 과정 을 거친다. 각 플레이어는 자신의 행동 이력(history)에 따라 정책(policy)을 선택하며, 이러한 정책의 조합을 공동 정책(Joint Policy) \(p = (p_1, p_2, ..., p_N)\) 라고 한다. 공동 정책을 통해 게임이 반복적으로 진행되며, 각 플레이어는 자신에게 최대한 유리한 학습 경로를 찾아가도록 학습 한다.
2. 최적 정책 학습 과정
확률 게임에서 각 플레이어는 최대 누적 보상(Expected Cumulative Reward) 을 얻기 위한 전략을 세운다. 각 플레이어 \(i\) 의 보상은 다음과 같이 정의된다.
\[V^{p, i}(u) = \mathbb{E}_p \left[ \sum_{t=0}^{M-1} \gamma^t r_i (u_t, a_t) | u_0 = u, p \right]\]여기서, \(V^{p, i}(u)\) 는 특정 상태 \(u\) 에서 플레이어 \(i\) 가 정책 \(p\) 를 따를 때 기대되는 누적 보상 값이다. \(\gamma\) 는 할인 계수로, 미래 보상의 중요도를 조절하는 값이다. 각 플레이어는 자신의 보상을 최대화하는 정책을 찾는 과정에서 최적 전략을 학습 하게 된다. 이 과정에서 최적 응답(Best Response, BR) 정책을 찾는 것이 핵심 목표가 된다.
\[p^*_i \in BR(p^{-i}) = \arg\max_{p_i} V^{p, i}(u) \quad \text{(given that other players' policies are fixed)}\]즉, 각 플레이어는 상대방의 전략이 고정된 상태에서 자신이 최대한 높은 보상을 얻을 수 있는 최적 정책을 찾는다.
3. 내쉬 균형 (Nash Equilibrium) 적용
이 게임에서 내쉬 균형(Nash Equilibrium) 이 존재한다는 것은, 모든 플레이어가 자신의 전략을 바꿔도 추가적인 이득을 얻을 수 없는 상태에 도달할 수 있다는 것을 의미 한다. 즉, \(p^* = (p^*_1, p^*_2, ..., p^*_N)\) 일 때, 어느 플레이어도 자신의 정책을 단독으로 변경하여 추가적인 보상을 얻을 수 없다.
내쉬 균형을 통해, 태스크 컨트롤러와 인간 인지 모델은 각각의 학습 전략이 수렴하는 최적 지점 을 찾게 된다.
4. 태스크 컨트롤러의 강화 학습 적용
태스크 컨트롤러는 Dueling Double Deep Q-Network (Dueling DDQN) 을 활용하여 학습된다. DDQN은 정책(policy)과 가치(value) 사이의 일관성을 유지하면서도 최적 학습 경로를 찾을 수 있도록 설계된 강화 학습 알고리즘 이다. DDQN의 업데이트 식은 다음과 같이 정의된다.
\[Y^{DDQN}_t = R_{t+1} + \gamma Q(s_{t+1}, \arg\max_a Q(s_{t+1}, a; \theta); \theta^-)\]여기서,
\(Q(s, a)\)`` 는 현재 상태에서 행동 \(a\)를 선택했을 때의 기대 보상을 의미한다. \(\theta^-\) 은 타겟 네트워크(target network) 파라미터이다.
5. 모델 학습 설정 및 하이퍼파라미터
태스크 컨트롤러는 DDQN을 사용하여 다양한 실험 조건에서 강화 학습을 수행 한다. 실험에서는 두 가지 수준의 지식 베이스(KB) 복잡도를 고려하였으며, 각 실험 조건에 따라 6개의 DDQN 에이전트를 학습 시켰다.
할인 계수(\(\gamma\)) = 0.99
학습률(\(\alpha\)) = 0.0001
타겟 네트워크 업데이트 빈도(\(\tau\)) = 0.001
배치 크기(\(\text{batch size}\)) = 32로,
각 에이전트는 100만 개의 에피소드(1M episodes) 를 경험하며 학습되었으며 각 에피소드에서 최대 100회의 상호작용을 수행하여 목표 상태에 도달하도록 학습 되었다.
태스크 생성
연구에서는 강화 학습을 통해 최적화된 태스크 컨트롤 정책(task control policy)을 이용하여 인과 학습 태스크(causal learning task)를 생성 하였다. 이 태스크 컨트롤 정책들은 훈련된 태스크 컨트롤러에서 샘플링(sampled) 되었으며, 실험에서 사용될 인과 학습 조건을 결정하는 역할을 한다. 연구진은 Bayesian+, Oneshot+, Oneshot-의 세 가지 태스크 컨트롤 정책을 학습된 태스크 컨트롤러에서 가져와서 태스크를 설계 하였다. 이 정책들은 두 가지 수준의 지식 베이스(Knowledge Base, KB) 복잡도를 기준으로 훈련되었으며,
단순 KB(Simple KB), 복잡한 KB(Complex KB) 두 가지 조건에서 각각 학습된 태스크 컨트롤러를 활용하여 총 6개의 최적화된 태스크 컨트롤 정책을 생성 하였다. 이후, 학습된 정책에서 무작위로 프레젠테이션 시퀀스(presentation sequences)를 샘플링하여 인과 학습 태스크를 구성 하였다. 단순 KB(Simple KB)에서는 단순 상태에서 훈련된 Bayesian+, Oneshot+, Oneshot- 컨트롤러에서 샘플링한 시퀀스를 사용하며, 복잡한 KB(Complex KB)에서는 복잡 상태에서 훈련된 Bayesian+, Oneshot+, Oneshot- 컨트롤러에서 샘플링한 시퀀스를 사용하였다.
각 인과 학습 태스크는 5개의 세션(session)으로 구성되며, 각 세션(session)에는 세 가지 다른 태스크 컨트롤 조건(Bayesian+, Oneshot+, Oneshot-)을 적용한 3개의 라운드(rounds)가 포함 된다. 즉, 참가자들은 총 15개의 독립적인 인과 학습 라운드를 수행 하게 된다. 다만, 이러한 태스크 컨트롤 시퀀스의 제시 순서는 참가자들이 특정 유형의 시퀀스를 인식하지 못하도록 의사 난수(pseudorandom) 방식으로 정해짐으로써 실험 참가자들은 자신이 Oneshot+ 또는 Bayesian+ 등의 특정 실험 조건에서 수행하고 있는지 인식하지 못하게 된다.
베이스라인 모델
연구진은 쉬운 태스크(easy tasks)에 대해서만 추가적으로 베이스라인 모델(baseline model) 을 사용하여 비교하였다. 이 베이스라인 모델은 “uniform” 모델 로, 각 S-O 관계를 무작위로 샘플링하여 제시하는 방식 이다. 예를 들어,
\[P = \{ S_1 O_1, S_2 O_2, S_3 O_1, S_4 O_2, S_5 O_3 \}\]와 같은 형태의 집합이 있다고 가정한다. 모델은 각 S-O 관계를 5번씩 샘플링하여 총 20개의 S-O 관계를 생성 한 후, 무작위 순서로 재배열하여 균등한(uniform) 방식으로 태스크를 생성 한다. 이후 실험에서 사용할 무작위(uniform) 시퀀스를 총 72개 생성 하고, 실험에서는 이 중 하나를 랜덤으로 선택하여 참가자들에게 제시하게 된다. 쉬운 태스크에서는 기존 3개의 태스크 컨트롤러(Bayesian+, Oneshot+, Oneshot-)에 uniform 모델을 추가하여, 총 4개의 실험 조건을 수행하였다. 즉, 각 세션에서 4개의 라운드(Bayesian+, Oneshot+, uniform, Oneshot-)를 포함 하도록 구성하였다.
실험 참가자들에게 제공된 태스크 지침 (Task Instruction)
각 세션은 여러 라운드(rounds)로 구성되며, 각각 쉬운 태스크는 4개의 라운드 (Bayesian+, Oneshot+, uniform, Oneshot-), 중간/어려운 태스크는 3개의 라운드 (Bayesian+, Oneshot+, Oneshot-)로 이루어진다. 각 라운드는 두 개의 단계로 이루어졌다.
인과 학습 단계(Causal Learning Phase)
이 단계에서는 참가자들이 태스크 컨트롤러가 제시하는 최적화된 실험 조건 에 따라, 특정한 S-O 관계(Stimulus-Outcome Pair) 를 반복적으로 관찰하며 인과적 관계를 학습하게 된다. 연구진은 참가자들이 충분히 인과 관계를 학습할 수 있도록 S-O 관계의 제시 횟수를 실험 난이도에 따라 조정 하였다. 쉬운 과제와 중간 난이도 과제에서는 S-O 관계가 각각 20번씩 제시되며, 어려운 과제에서는 학습이 더욱 복잡해지도록 S-O 관계가 36번 제시된다.
S-O 관계는 각각 두 개의 이미지 로 이루어지며, 첫 번째 이미지는 자극(Stimulus, S), 두 번째 이미지는 결과(Outcome, O) 역할을 한다. 참가자들은 이 관계를 반복적으로 관찰하며 S가 O를 유발하는지 학습 하게 된다.
실험에서 사용된 이미지는 프랙탈 이미지(fractal images) 로, 참가자들의 사전 지식이나 선호도가 인과 학습에 영향을 미치지 않도록 설계되었다. 연구진은 총 127개의 프랙탈 이미지 데이터셋 을 구축하였으며, 참가자들이 매 라운드에서 무작위로 선택된 이미지들을 학습하도록 설계 하였다. 또한, 연속된 S-O 관계가 지나치게 강하게 연결되지 않도록, 각 S-O 관계 사이에는 공백(nil presentation) 구간 을 삽입하여 참가자들이 개별적인 관계를 독립적으로 학습하도록 유도하였다.
S-O 관계의 제시 시간은 난이도에 따라 다르게 설정되었다. 쉬운 과제에서는 고정된 시간 을 사용하여, 자극과 결과 이미지는 각각 0.7초 동안 제시된 후, 1.5초 동안 공백 상태 가 유지되었다. 반면, 중간 및 어려운 과제에서는 S-O 관계의 노출 시간이 무작위로 변화 하였으며, 자극과 결과 이미지는 0.3~0.6초 사이에서 랜덤하게 제시되었고, 공백 시간도 0.6~1.2초 범위에서 무작위로 결정 되었다. 이는 난이도가 증가할수록 정보 제공 시간이 줄어들어 학습이 더 어려워지는 환경을 조성하기 위함 이었다.
평가 단계(Rating Phase)
참가자들은 인과 학습이 끝난 후, S-O 관계에 대한 신뢰도를 평가하는 과정 을 수행하였다. 이 단계에서 참가자들은 결과(Outcome)와 자극(Stimulus) 사이의 인과적 연결 강도를 정량적으로 평가 해야 했다.
쉬운 과제와 중간 난이도 과제에서는 3개의 평가 항목이 주어졌으며, 이는 단순한 인과 관계를 평가할 수 있도록 설계되었다. 반면, 어려운 과제에서는 더 복잡한 인과적 연결을 평가할 필요가 있기 때문에 4개의 평가 항목이 제공 되었다. 이 평가 항목들은 결과가 직접적으로 연결된 자극뿐만 아니라, 간접적으로 연결된 자극까지 포함하도록 설계 되었다.
참가자들은 각각의 인과 관계에 대해 0점 (“전혀 연관 없음”) ~ 10점 (“매우 강한 인과 관계”) 의 척도로 평가를 수행하였다. 이 평가값은 1점 단위(step size)로 증가할 수 있도록 설정되었으며, 참가자들은 각 자극이 특정 결과를 유발했다고 믿는 정도를 점수로 나타내야 했다. 이 평가 과정에서, 참가자들이 단순히 기억에 의존하여 정답을 고르지 못하도록 실제 실험 조건에 존재하지 않는 무작위 이미지도 평가 항목에 포함 되었다.
쉬운 과제와 중간 난이도 과제에서는 각 평가에서 참가자들에게 8개의 자극 이미지가 제공 되었다. 이 중 5개는 실제 인과 관계가 존재하는 이미지였으며, 3개는 연구진이 랜덤하게 추가한 무작위 자극 이미지 였다. 어려운 과제에서는 각 평가에서 16개의 자극 이미지가 제공 되었다. 이 중 15개는 실제 실험에 포함된 이미지였으며, 나머지 1개는 실험에 존재하지 않는 무작위 자극 이미지 였다.
이렇게 무작위 이미지를 추가함으로써, 참가자들이 단순히 기억력에 의존하여 평가하는 것이 아니라, 실제 인과 관계를 학습하고 논리적으로 판단하는지 검증할 수 있도록 설계되었다.
자극 및 결과 이미지(Stimulation and Outcome Images) 구성
연구에서 사용된 자극(Stimuli)과 결과(Outcomes) 이미지 데이터셋은 총 127개의 프랙탈 이미지로 구성되었는데, 이러한 프랙탈 이미지는 기존의 사물 이미지와 달리 참가자의 사전 지식이나 선호도의 영향을 받지 않도록 설계된 시각적 자극 이다.
각 참가자는 실험 시작 시 컴퓨터가 무작위로 선택한 프랙탈 이미지 세트를 배정받았으며, 이후 각 라운드에서도 무작위로 이미지가 선택되지만, 이전 라운드에서 사용된 이미지는 중복되지 않도록 구성 되었다. 이러한 샘플링 방식은 참가자들이 특정 이미지를 반복적으로 보면서 생기는 기억 효과(carry-over effect)를 방지 하기 위함이다.
쉬운 및 중간 난이도 과제(Easy & Medium Tasks)에서의 이미지 구성
쉬운 과제와 중간 난이도 과제는 단순한 지식 베이스(Knowledge Base, KB)를 사용 하였다. 따라서 각 참가자는 총 15개의 프랙탈 이미지 세트를 사용하여 15개의 라운드를 수행 하였다. 즉 라운드별로 이미지 세트는 중복되지 않는다. 이를 통해 모든 참가자가 동일하게 새로운 이미지를 경험하도록 보장 하고, 기억 효과(carry-over effect)가 학습 과정에 영향을 미치지 않도록 통제 하였다.
각 프랙탈 이미지 세트는 자극 이미지 5개, 결과 이미지 3개 총 8개의 이미지로 구성하였고, 총 5개의 세션이 3라운드 동안 진행되므로 이러한 구성을 통해 각 참가자는 총 120개의 이미지를 보게 된다. (계산식: 8개 × 3 라운드 × 5 세션 = 120개 이미지)
어려운 과제(Difficult Task)에서의 이미지 구성
어려운 과제는 보다 복잡한 지식 베이스(Complex KB)를 사용 하므로, 이미지 샘플링 방식이 쉬운 및 중간 난이도 과제와 약간 다르게 설계되었다.
각 참가자는 15개의 프랙탈 이미지 세트를 사용하여 15개의 라운드를 수행하며, 각 라운드(round)에서는 17개의 프랙탈 이미지가 사용되기 때문에 한 세션에서 3라운드를 진행하므로 한 세션(session)당 51개의 프랙탈 이미지가 필요하다. 각 세션 시작 시, 컴퓨터가 데이터셋에서 51개의 프랙탈 이미지를 무작위로 선택하되 이전 세션에서 사용한 프랙탈 이미지는 포함되지 않도록 제한하였다. 그리고 각 라운드에서는 51개 이미지 중 17개를 추가적으로 무작위 선택하여 사용하되 이전 라운드에서 사용한 이미지는 중복되지 않도록 제한하였다. 이러한 방식으로 두 개의 연속된 세션에서는 중복된 이미지가 등장하지 않도록 설정하였다.
또한 연구진은 참가자가 특정 이미지를 반복적으로 보면서 생길 수 있는 기억 효과를 최소화하기 위해 다양한 통제 전략을 적용 하였다. 한 세션에서 사용된 이미지는 다음 세션까지 등장하지 않도록 설계하고, 각 라운드에서도 중복된 이미지를 피하기 위해 무작위 샘플링 진행하였다. 최악의 경우, 참가자가 동일한 이미지를 다시 보게 되는 상황이 발생하더라도, 적어도 3개의 독립적인 라운드(총 51개의 다른 프랙탈 이미지)를 학습한 후에야 동일한 이미지가 다시 나타나도록 설계하였다. 연구진은 이러한 설계 방식을 통해, 설사 동일한 이미지가 두 세션 사이에서 재사용되더라도, 참가자의 인과 학습에 미치는 영향이 거의 없음을 보장 하였다.
또한, 실험 참가자들에게 각 라운드는 서로 독립적이라는 점을 사전에 안내하여, 참가자가 특정 이미지를 기억하려는 의도를 가지지 않도록 유도 하였다. 이러한 조치는 프랙탈 이미지가 실험 과정에서 새로운 시각적 자극으로 유지되도록 하기 위함이며, 참가자가 인과 학습을 수행하는 과정에서 기억 효과가 개입하지 않도록 통제하는 핵심 전략이다.
연결성 정도 (Degree of Connectivity) 및 태스크 수행 측정(Task Performance Measures) 설명
연구에서는 태스크 컨트롤러가 학습된 인과 관계를 어떻게 연결하는지(연결성 정도)와 참가자들의 태스크 수행 능력을 정량적으로 평가하는 방법 을 설명하고 있다. 연결성 정도는 자극(Stimulus)과 결과(Outcome) 간의 연결이 얼마나 복잡하게 이루어지는지를 나타내며, 태스크 수행 능력은 참가자들이 인과 관계를 얼마나 정확하고 효율적으로 학습했는지 평가하는 지표 로 측정되었다.
1. 연결성 정도 (Degree of Connectivity)
연결성 정도는 그래프 이론(Graph Theory)의 개념에서 노드(Node)에 연결된 엣지(Edge)의 수를 의미 한다. 즉, 특정 노드가 다른 노드와 얼마나 많은 연결을 맺고 있는지를 나타내는 지표이다. 연구에서는 노드(Node)는 S-O 관계(Stimulus-Outcome Pair), 엣지(Edge)는 인과적 연결(Causal Relationship)으로 하는 지식 베이스(Knowledge Base, KB)를 그래프 구조로 모델링 하였다.
일반적인 연결성 정도의 정의는 각 노드에서 직접 연결된(outgoing) 엣지의 개수 를 의미한다. 하지만 연구에서는 단순한 직접 연결뿐만 아니라, “자식 노드(child nodes)”의 모든 연결도 포함하여 연결성 정도를 확장 하였다. 이러한 방식은 참가자들이 직접적인 인과 관계뿐만 아니라, 간접적인 인과 관계도 학습하는 상황을 고려하기 위함 이다.
연결성 정도는 아래의 수식으로 정의된다.
\[\text{degree}_G(n_r) = \sum_{i=1}^{N} d^{i-1} \sum_{j=1}^{K} \text{degree}(n_j^{c_i})\] \[\begin{aligned} \text{degree}(n) = \text{Number of outgoing edges from node } n \\ n_r = \text{Root node (Outcome node)} \\ n_j^{c_i} = \text{j-th child node at layer } i \\ d = 0.5 \quad \text{(Discount factor)} \end{aligned}\]이렇게 연결성 정도는 특정 결과(Outcome) 노드에서 출발하여 자식 노드들의 모든 연결을 고려하는 방식으로 계산 되었다.
2. 태스크 수행 측정 (Task Performance Measures)
연구에서는 참가자의 인과 학습 성과를 평가하기 위해 3가지 지표 를 사용하였다.
- 인과 평가 점수 (Causal Ratings)
참가자가 각 S-O 관계에 대해 얼마나 강한 인과적 연관성을 느끼는지 평가한 점수로, 점수가 높을수록 참가자가 해당 S-O 관계를 더 강하게 인과적으로 연결하고 있다고 판단하였다. 원본(raw) 신뢰도 점수로 사용 되며, 정규화되지 않은 점수이다
- 테스트 점수 (Test Scores)
테스트 점수는 인과 평가 점수(Causal Rating)를 정규화(normalized)하여 비교 가능하도록 변환한 값 이다. 즉, 참가자가 특정 S-O 관계에 대해 부여한 점수가 다른 관계들과 비교했을 때 상대적으로 얼마나 높은지를 정량화 하는 지표이다.
\[\begin{aligned} t_i = \frac{c_i}{c_0} \\ c_0 = \sum_{j=1}^{N} c_j \end{aligned}\]여기서 \(t_i\)는 \(i\)번째 S-O 관계의 테스트 점수, \(c_i\)는 해당 S-O 관계에 대한 참가자의 인과 평가 점수, \(c_0\)는 전체 S-O 관계의 총 인과 평가 점수이다.
어떤 참가자가 S1-O1 관계와 S2-O1 관계에 각각 10점을 부여했다고 가정 하면, 원본 인과 평가 점수는 (S1-O1 = 10, S2-O1 = 10),
\[\begin{aligned} c_0 = 10 + 10 = 20 \\ t_{S1-O1} = \frac{10}{20} = 0.5 \\ t_{S2-O1} = \frac{10}{20} = 0.5 \\ \end{aligned}\]즉, 참가자가 동일한 점수를 부여했더라도, 해당 관계가 전체 관계들 속에서 상대적으로 어느 정도의 중요성을 가지는지를 나타내는 지표이다.
- 학습 효율성 (Learning Efficiency)
학습 효율성은 S-O 관계가 제시된 횟수 대비 참가자가 인과적 학습을 얼마나 효과적으로 수행했는지를 평가하는 지표 이다. 즉, 한 번의 S-O 관계 제시에서 얼마나 많은 학습이 이루어졌는지를 정량화 한다.
\[l_i = \frac{t_i}{n_i}\]여기서 \(l_i\)는 \(i\) 번째 S-O 관계의 학습 효율성, \(t_i\)는 해당 S-O 관계의 테스트 점수, \(n_i\)는 해당 S-O 관계가 제시된 횟수이다. 예를 들어 S1-O1 관계가 4번 제시되었고, 테스트 점수가 5였을 경우
\[l_{S1-O1} = \frac{5}{4} = 1.25\]위의 결과를 통해 한 번 제시될 때마다 평균적으로 1.25만큼 학습이 이루어졌다고 말할 수 있다. 또 S1-O1 관계가 1번 제시되었고, 테스트 점수가 5였을 경우
\[l_{S1-O1} = \frac{5}{1} = 5.0\]이 경우 단 한 번의 노출로도 높은 학습 성과를 얻었음을 의미하며, 학습 효율성이 높은 경우 로 해석할 수 있다.
효과 크기 (Effect Size) 및 설정 변수
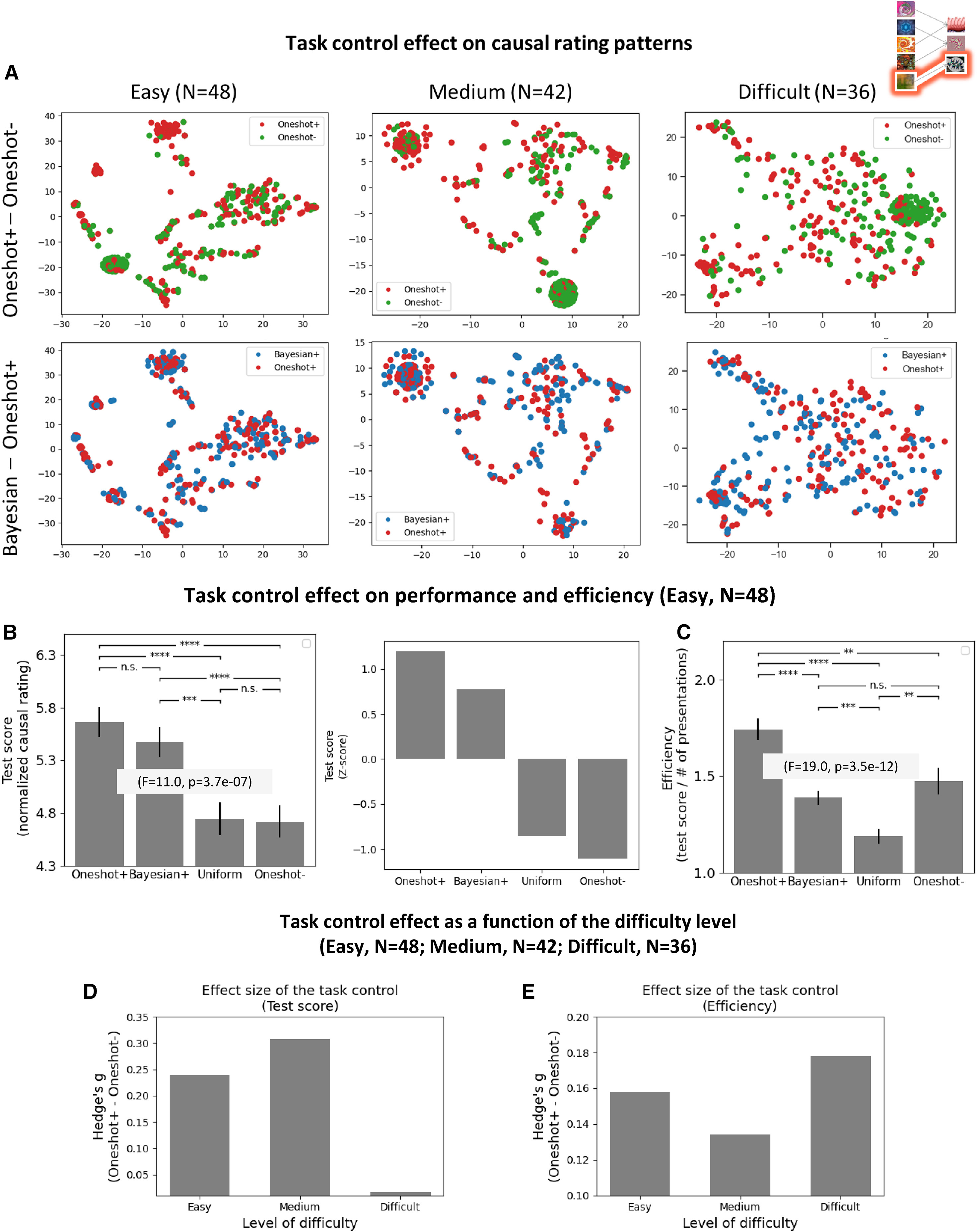
태스크 컨트롤러의 효과를 평가하기 위해 조건별 수행 차이를 정량적으로 비교 하였다. 특정 태스크 컨트롤 조건들 간의 차이를 평가하기 위해 Hedge’s g 효과 크기(effect size)를 사용 하였다.
\[\text{Effect Size} = \frac{\text{Mean difference between conditions}}{\text{Pooled standard deviation}}\]비교 조건은 각각 Oneshot+ 조건 vs. Oneshot- 조건, Uniform 조건 vs. Oneshot- 조건이며 효과 크기가 클수록 태스크 컨트롤이 참가자의 인과 학습 수행에 더 큰 영향을 미쳤음을 의미 한다.
실험에서 사용된 주요 변수와 설정값은 다음과 같다.
\[\begin{aligned} \gamma = 0.99 \quad \text{(Discount factor)} \\ \alpha = 0.0001 \quad \text{(Learning rate)} \\ \tau = 0.001 \quad \text{(Target network update frequency)} \\ \text{batch size} = 32 \end{aligned}\]One-shot Inference Bias 분석
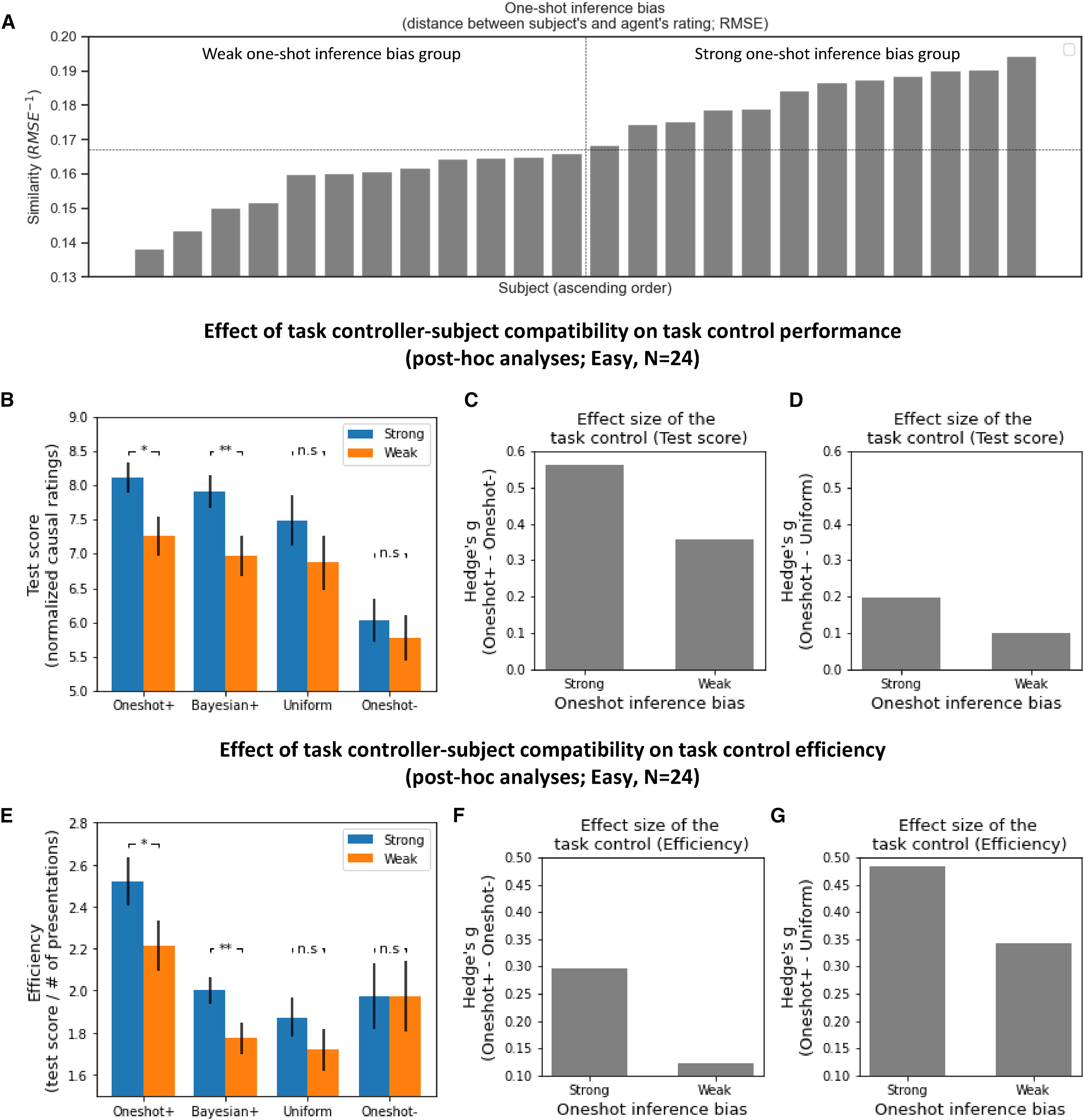
연구에서는 참가자의 One-shot inference bias(일회적 추론 편향)를 측정하여 참가자와 모델 간의 유사도를 평가하였다. 이는 개인이 점진적 학습보다 일회적 인과 추론을 얼마나 선호하는지를 반영하는 지표로 정의된다. 특히, 연구에서는 Oneshot+ 조건에서 사용된 인과 추론 모델과 참가자의 인과 평가 점수 간의 유사도를 비교하여 이를 측정하였다.
One-shot inference bias를 측정하기 위해 연구진은 먼저 Baseline 모델(Uniform Sequence) 조건에서 참가자의 인과 평가 점수를 수집하였다. 이 조건에서는 참가자들이 특정 태스크 컨트롤 없이 무작위로 생성된 시퀀스를 기반으로 학습하게 된다. 이후 동일한 uniform 시퀀스를 Oneshot+ 모델에도 적용하여 모델이 생성한 인과 평가 점수를 수집하였다. 이때 Oneshot+ 모델은 인간 참가자가 아닌 인공지능 기반의 인과 추론 모델로, Oneshot+ 조건에서 최대한 일회적 인과 추론을 유도하도록 설계되었다.
두 그룹(참가자와 모델)의 인과 평가 점수를 비교하기 위해 Root Mean Square Error(RMSE)를 계산하였다. 이때 RMSE 값의 역수를 One-shot inference bias로 정의하였으며, RMSE 값이 작을수록 참가자와 Oneshot+ 모델 간의 유사성이 높다는 것을 의미한다. 따라서 RMSE가 낮을수록 해당 참가자는 일회적 인과 추론을 더 선호하는 경향을 보인다고 해석할 수 있다.
딥러닝 기반 RL 프레임워크의 목표 행동 유도 효과 분석
연구에서는 딥러닝 기반 강화학습(RL) 프레임워크가 참가자의 목표 행동을 효과적으로 유도할 수 있는지를 검증하였다. 이를 위해 연구진은 Uniform 시퀀스와 Control 시퀀스 간의 유사도와 수행 결과의 관계를 분석하였다.
Uniform 시퀀스는 무작위로 생성된 시퀀스를 의미하며, Control 시퀀스는 RL 모델이 최적화한 시퀀스를 의미한다. 연구에서는 두 시퀀스 간의 거리를 RMSE로 계산하였으며, 두 시퀀스 간 거리가 작을수록 학습 성과가 더 높을 것으로 예상하였다. 분석 결과, RMSE가 작은 그룹일수록 수행 성과(Causal Ratings, Test Scores)가 유의미하게 더 높게 나타났다.
추가적으로, 연구진은 Uniform 시퀀스를 두 개의 그룹으로 나누어 비교하였다. 첫 번째 그룹은 RMSE가 50분위수(percentile)보다 작은 그룹이며, 두 번째 그룹은 그보다 큰 그룹이었다. 비교 결과, RMSE가 작은 그룹이 더 높은 학습 성과를 보였다. 또한 이 결과는 시퀀스를 더 세분화하여 4개 그룹으로 분류하였을 때도 동일한 경향을 나타냈다.
이러한 결과는 기존의 단순한 실험 설계 방식과 비교했을 때, 딥러닝 기반 태스크 컨트롤 방식이 훨씬 효과적으로 목표 행동을 유도할 수 있음을 시사한다. 연구진은 본 연구의 모델 기반 태스크 설계가 기존 방식보다 여러 가지 장점을 가진다고 주장하였다. 첫째, 목표 지향적으로 특정 학습 조건(예: Oneshot+ 또는 Bayesian+)을 설정할 수 있다. 둘째, 수행 데이터를 기반으로 정량적으로 평가할 수 있다. 셋째, 다양한 환경에서 일반화 가능하고, 예측 가능성을 높일 수 있다. 마지막으로, 설명 가능한 AI 기술을 적용하여 태스크 컨트롤의 원리를 해석할 수 있다.
결론적으로, 연구 결과는 딥러닝 기반 RL 태스크 컨트롤이 참가자의 학습 패턴을 효과적으로 조절할 수 있으며, 무작위 태스크 설계보다 우월한 조절 능력을 가졌음을 보여준다.
Logistic Regression 분석을 통한 태스크 컨트롤 조건 예측
연구진은 Logistic Regression(로지스틱 회귀 분석)을 수행하여 태스크 컨트롤 조건을 참가자의 신뢰도 평가(confidence ratings)만으로 예측할 수 있는지를 검증하였다. 독립 변수는 참가자가 특정 S-O 관계의 강도를 평가한 인과 신뢰도 점수(Causal Ratings)였으며, 종속 변수는 태스크 컨트롤 조건(Task Control Condition: Bayesian+, Oneshot+, Oneshot-)이었다. 연구에서는 3가지 난이도(Easy, Medium, Difficult)와 3가지 컨트롤 조건(Bayesian+, Oneshot+, Oneshot-)을 조합하여 총 9개의 로지스틱 회귀 모델을 학습하였다.
분석 결과, 특정 새로운 S-O 쌍(Novel S-O Pair)의 신뢰도 점수는 Oneshot+ 조건을 예측하는 데 중요한 역할을 하였다. 특히, Easy & Medium 난이도에서는 β3 (b3), Difficult 난이도에서는 β4 (b4) 파라미터가 유의미한 영향을 미쳤다. 이는 참가자가 새로운 S-O 관계에서 높은 신뢰도를 보일수록 Oneshot+ 학습 경향이 강하다는 것을 시사한다.
반면, 기존 일반적인 S-O 쌍(Ordinary S-O Pairs)의 신뢰도 점수는 Bayesian+ 조건을 예측하는 데 중요한 역할을 하였다. Easy & Medium 난이도에서는 β2 (b2), Difficult 난이도에서는 β3 (b3) 파라미터가 유의미하게 작용하였다. 즉, 참가자가 기존의 S-O 관계에서 신뢰도를 더 높게 평가할수록 Bayesian+ 방식으로 학습하는 경향이 나타났다.
흥미로운 점은 Oneshot- 조건에서 관찰된 결과였다. Oneshot-의 목표는 참가자의 학습 수행을 방해하는 것이었으며, 이를 위해 특정 S-O 관계에서 학습률(Learning Rate)을 거꾸로 설정하는 방식이 사용되었다. 즉, 이미 학습이 잘 된 관계의 학습률을 더 높이고, 반대로 학습되지 않은 관계는 적게 노출되도록 설계되었다. 이로 인해 참가자는 특정 관계에 대한 신뢰도를 과도하게 높이거나 특정 관계를 무시하는 경향을 보였다. 분석 결과, Easy & Difficult 난이도에서는 일반적인 S-O 관계에 대한 신뢰도가 높아졌으며, Medium 난이도에서는 새로운 S-O 관계에 대한 신뢰도가 낮아지는 패턴이 관찰되었다.
이러한 결과는 참가자의 신뢰도 평가 점수만으로도 태스크 컨트롤 조건을 예측할 수 있으며, Oneshot+ 학습자는 새로운 S-O 관계에서 높은 신뢰도를 보이고, Bayesian+ 학습자는 기존 관계에서 높은 신뢰도를 보인다는 점을 확인시켜 준다. 또한 Oneshot- 조건에서는 참가자의 신뢰도 패턴이 왜곡되어 학습 수행이 방해된다는 점을 보여준다.
방법론 설명이 길어져 결과 해석은 다음 포스트에서 진행하겠다.