Linear reinforcement learning in planning, grid fields, and cognitive control

이 논문에서는 인간의 유연한 계획 능력과 반대로 비유연적인 습관적 행동을 설명하는 데 있어서, 과거 연산의 재사용(reuse of previous computation)이라는 개념을 중심으로 한 새로운 모델을 제안한다.

기존에는 model-based 방법론이 유연한 행동을 설명하고, model-free 방법론이 습관을 설명했으나, model-based 계획은 계산적으로 복잡하고, model-free는 유연한 재계획(replanning)을 설명하지 못하는 등 이 두 방식 모두 뇌의 행동을 완전히 설명하는 데에는 한계가 있었다.

이에 저자들은 control engineering에서 영감을 받아, 미래 사건에 대한 시간적으로 추상화된 지도를 재사용(temporally abstracted map of future events)하여 유연한 선택을 가능하게 하면서도 특정한, 정량화 가능한 편향(bias)을 유도하는 생물학적으로 그럴듯한 모델을 제안한다.

이 모델은 고전적인 비선형 최적화 대신, default policy를 기준으로 하는 soft한 선형 근사(linear approximation)를 사용해 최적화한다. 이 default policy에 약한 편향이 들어감으로써, 이 모델은 유연한 재계획과 인지 통제(cognitive control) 같은 행동신경과학 현상들을 연결지을 수 있게 된다.

Introduction

전통적인 강화학습 모델은 유연한 행동(예: 재계획, goal 변경)에 대해서는 model-based 접근을, 비유연적인 행동(예: 습관, 중독, Pavlovian 편향)에 대해서는 model-free 접근으로 설명해 왔다. 그러나 이 모델들은 유연성과 비유연성 모두를 동시에 설명하지는 못한다는 한계가 있다.

Model-based 접근은 미래 행동을 계획하기 위해 Bellman 방정식을 반복적으로 풀어야 하며, 이는 계산량이 너무 커서 생물학적으로 비현실적이다. 반면 model-free 접근은 과거에 학습한 행동 선호도를 캐시해 두고 재사용하지만, 이는 정책 변경이나 보상의 변화에 적응하는 데에 한계가 있다. 이에 따라 기존 연구에서는 successor representation (SR)을 활용하여 일정 수준의 재계획 가능성을 확보했지만, SR 역시 기존 정책에 종속되어 있어 목표(goal)나 행동 경로가 크게 바뀌는 경우 적절한 재계산이 어렵다는 한계를 가진다.

이러한 한계를 극복하기 위해 저자들은 control engineering 분야에서 제안된 linearly solvable MDP (LMDP)에 기반하여, SR과 유사하지만 보다 안정적이고 범용적인 Default Representation (DR) 개념을 도입한다. DR은 default policy 하에서의 미래 상태 방문 기대치를 저장한 행렬로, 이는 정책이 변경되더라도 변하지 않는 안정적인 기저(reusable map) 역할을 하며, 목표 변경에 따른 유연한 계획도 가능하게 한다. 핵심 아이디어는 정확한 최적화를 대신해 default policy로부터의 편차를 비용으로 반영하는 soft한 최적화 방식을 도입함으로써, Bellman 방정식을 선형 형태로 근사하고 생물학적으로 plausibility를 유지한다는 점이다.

이러한 방식은 entorhinal grid cell과 border cell의 역할에 대한 새로운 해석도 가능하게 한다. Grid cell은 과제 공간의 Fourier-like 표현을 제공하는 것으로 해석될 수 있으며, DR은 이러한 반복적인 공간 구조를 기반으로 동작할 수 있다. 반면 환경에 경계가 생겼을 때는 DR이 새로운 기저 함수로 업데이트되며, 이는 border cell의 응답 특성과 대응된다.

또한 Linear RL은 유연한 계획만이 아니라, 왜 특정 상황에서는 비유연하거나 편향된 행동이 발생하는지도 설명한다. 예를 들어, Stroop task나 Pavlovian 편향 같은 현상은 default policy에서 벗어나는 데 드는 비용으로 해석되며, 이는 인지 통제(cognitive control)의 부담(cost of control)을 수치적으로 설명하는 근거가 된다. 따라서 Linear RL은 단순한 모델임에도 불구하고, 행동 신경과학에서 관찰되는 다양한 현상들을 하나의 이론적 틀로 통합적으로 설명할 수 있다.

Results

The model

이 논문에서는 고전적인 마르코프 결정 과정(MDP)에서 발생하는 순차적 의사결정 문제의 복잡성을 해결하기 위한 새로운 접근법으로 linear RL 모델을 제안한다. 일반적인 강화학습 문제에서는 에이전트가 상태 $s_t$에서 행동 $a_t$를 선택하고, 이에 따라 다음 상태로 전이하며 보상 $r_t$를 받는다. 에이전트의 목표는 미래 보상의 총합, 즉 value function \(v^*(s)\)를 최대화하는 것이다.

전통적인 방식에서는 최적 value 함수 \(v^*(s)\)는 Bellman 방정식을 통해 재귀적으로 정의되며, 각 상태에서의 최적 행동은 미래의 모든 선택에 의존하게 된다:

\[v^*(s_t) = r(s_t) + \max_{a_t} \sum_{s_{t+1}} P(s_{t+1} | s_t, a_t) v^*(s_{t+1})\]

하지만 이러한 계산은 큰 상태 공간에서는 매우 비효율적이며, 실제 생물학적 시스템이 이를 그대로 구현하기에는 부담이 크다. 이에 대한 한 가지 해결책은 정책 $\pi$가 고정되었다고 가정하고, 그에 따라 미래 상태 방문 기대치를 계산하는 Successor Representation (SR)이다. SR을 이용하면 다음과 같이 간단한 선형 방정식으로 표현된다:

\[v^\pi = S^\pi r\]

여기서 $S^\pi$는 정책 $\pi$ 하에서 시작 상태로부터 미래에 어떤 상태를 방문할 기대치를 담고 있는 행렬이다. 하지만 SR은 현재 정책 $\pi$ 하에서의 예측만 가능하므로, 목표가 바뀌어 최적 정책 \(\pi^*\)가 달라지면 정확한 의사결정을 할 수 없다.

이에 대해 linear RL은 최적 정책 \(\pi^*\) 자체를 선형적으로 근사할 수 있는 모델을 제안한다. 핵심은 정확한 최적화를 하지 않고, default policy $\pi_d$로부터의 편차를 비용으로 간주하는 방식이다. 이렇게 하면 max 연산이 제거되며, 아래와 같이 지수 함수 형태의 선형 방정식으로 value function을 표현할 수 있다:

\[\exp(v^*) = M P \exp(r)\]

여기서

• \(v^*\): 각 상태에서의 최적 가치 함수 (보상 - 제어 비용)
• $r$: terminal state(목표 상태)에서의 보상 벡터
• $P$: 각 nonterminal 상태에서 terminal 상태로 도달할 확률
• $M$: Default Representation (DR) 행렬로, default policy $\pi_d$ 하에서 nonterminal 상태 간의 ‘가까움’을 측정하는 값이다.

DR은 SR과 비슷하지만, SR이 특정 정책 $\pi$에 종속된 반면 DR은 default policy $\pi_d$ 하에서 계산되므로 다양한 목표 변화에 안정적으로 재사용 가능하다. DR은 특정 목표 $r$가 주어지면 그에 대응하는 최적 policy \(\pi^*\)를 쉽게 계산할 수 있도록 한다. 이는 특히 replanning, reward 변화, goal 전환 등의 상황에서도 유연하게 대응할 수 있게 해 준다.

또한 max 연산을 log-sum-exp로 근사하는 방식(log-average-exp)은 soft한 최적화를 가능하게 하고, 이는 Pavlovian 편향이나 인지 통제 비용 같은 행동 편향을 자연스럽게 설명하는 기반이 된다. DR은 grid cell 기반의 공간 표현, border cell의 응답 방식 등 뇌에서의 공간적/정신적 탐색에도 연관될 수 있는 잠재력을 지닌 표현 구조이다.

결론적으로, linear RL은 강화학습에서의 정책 간 상호의존성 문제를 부드럽게 근사하는 선형 모델로 볼 수 있다.

Model performance

핵심 아이디어는 이 모델이 최적 정책을 계산할 때 기대 보상(reward)과 제어 비용(control cost) 사이의 균형을 추구한다는 점이다. 이로 인해 linear RL은 deterministic한 정책이 아니라 softmax와 유사한 stochastic policy를 생성하게 된다(Fig. 1a, b).

figure 1. The linear RL model. a, b The model optimizes the decision policy by considering the reward and the control cost, which is defined as the KL divergence between the decision policy and a default policy. Assuming an unbiased (uniform) distribution as the default policy, the optimal decision policy balances the expected reward with the control cost. Although the expected reward is maximum when probability of choosing A is close to 1 (and therefore probability of choosing B is about zero), this decision policy has maximum control cost due to its substantial deviation from the default policy. The optimal value instead maximized expected reward minus the control cost, which here occurs when probability of choosing A is 0.73. c, d The model accurately approximates optimal choice. We compared its performance on a seven-level decision tree task (with random one-step costs at each state) to six pruned model-based RL algorithms, which evaluate the task to a certain depth (D = 1,..,6; D7 is optimal; D1 is equivalent to the successor representation for the random walk policy) and use average values at the leaves. Linear RL (LRL) achieved near-optimal average costs (y-axis is additional cost relative to the optimum). Local costs of all states were randomly chosen in the range of 0–10, and simulations were repeated 100 times. Mean, standard error of the mean, and distribution of data across 100 simulations are plotted. Source data are provided as a Source Data file.

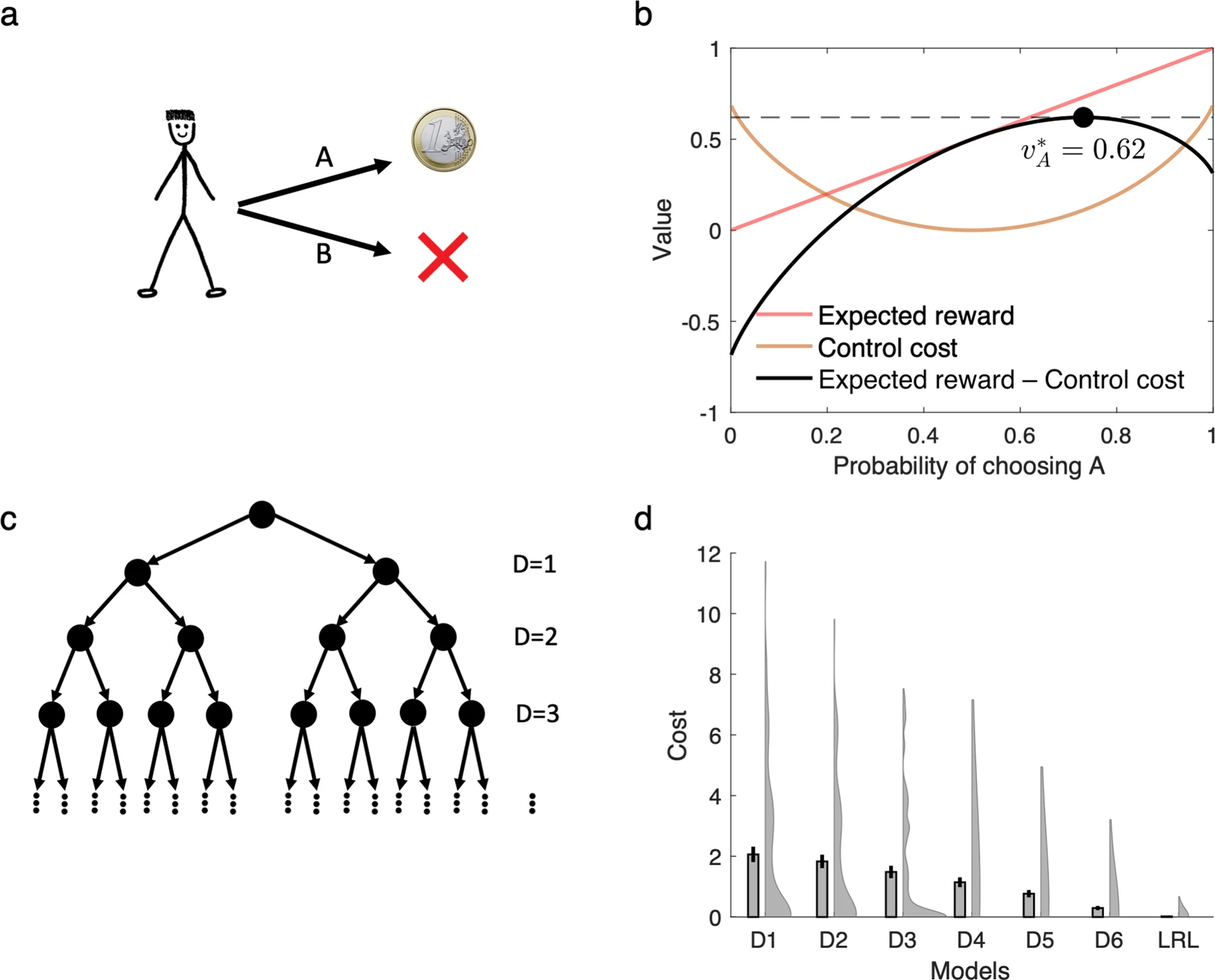
모델 성능을 평가하기 위해 저자들은 7단계로 구성된 어려운 의사결정 트리 환경을 사용했다. 이 환경에서 각 상태는 두 개의 후속 상태로 전이될 수 있으며, 각 상태에는 무작위 비용이 할당된다. 목표는 루트 상태에서 리프까지 도달하는 최소 비용 경로를 찾는 것이다. Linear RL은 다음과 같은 다양한 baseline 모델들과 비교되었다:

• 정확한 모델 기반 계획 (exact model-based solution)

• 깊이에 따른 가지치기(planning with pruning)를 수행하는 근사적 모델 기반 에이전트들: 이들은 특정 깊이까지는 정확하게 평가하지만, 그 이후에는 남은 서브트리의 평균값을 대체하여 계산을 단순화한다. 이 방식은 1-step 가지치기 시 SR (Successor Representation)과 동일하며, SR은 uniform random policy를 따르는 것으로 해석된다(Fig. 1c).

Linear RL에서는 default policy $\pi_d$를 uniform distribution으로 고정하고, 이를 모든 시뮬레이션에 공통적으로 사용하였다. 이는 SR처럼 매 task에서 default policy를 다시 학습하거나 업데이트해야 하는 필요성을 제거하고, linear RL이 얼마나 일반화된 재계획(replanning)을 가능하게 하는지를 보여준다. 그 결과, linear RL은 거의 최적에 가까운 평균 비용 성능을 달성했다(Fig. 1d).

중요한 점은 linear RL에서 사용하는 Default Representation (DR) 행렬 $M$은 task의 구조(즉, nonterminal state 간의 거리 정보 등)를 반영하며, reward 값 $r$이나 특정 목표(goal)에 종속되지 않는다는 점이다(Fig. 2). 따라서 DR을 한 번 계산하거나 학습해 두면, goal reward가 변하거나 새로운 목표가 생겼을 때도 재계획이 매우 효율적으로 수행될 수 있다. 이는 공간적 과제(spatial tasks)에서 임의의 상태에서 임의의 목표 상태로의 최단 경로를 찾는 것과 같은 역할을 한다.

figure 2. Default representation. a The DR corresponding to a three-level decision tree task is shown. Each row of the DR represents weighted future expectancies starting from the corresponding state and following the default policy. Therefore, the DR is independent of the goals and optimized policy. b, c The optimized path for planning from home (H) to the food (F) state is computed based on the DR. The linear RL model is efficient because the same DR is sufficient for planning towards a new goal, such as the water (W) state. d The path between every two states in a 10 × 10 maze environment (d) computed by linear RL exactly matches the optimal (shortest) path computed by exhaustive search. The DR has been computed once and reused (in combination with techniques from matrix identities) to compute each optimal path.

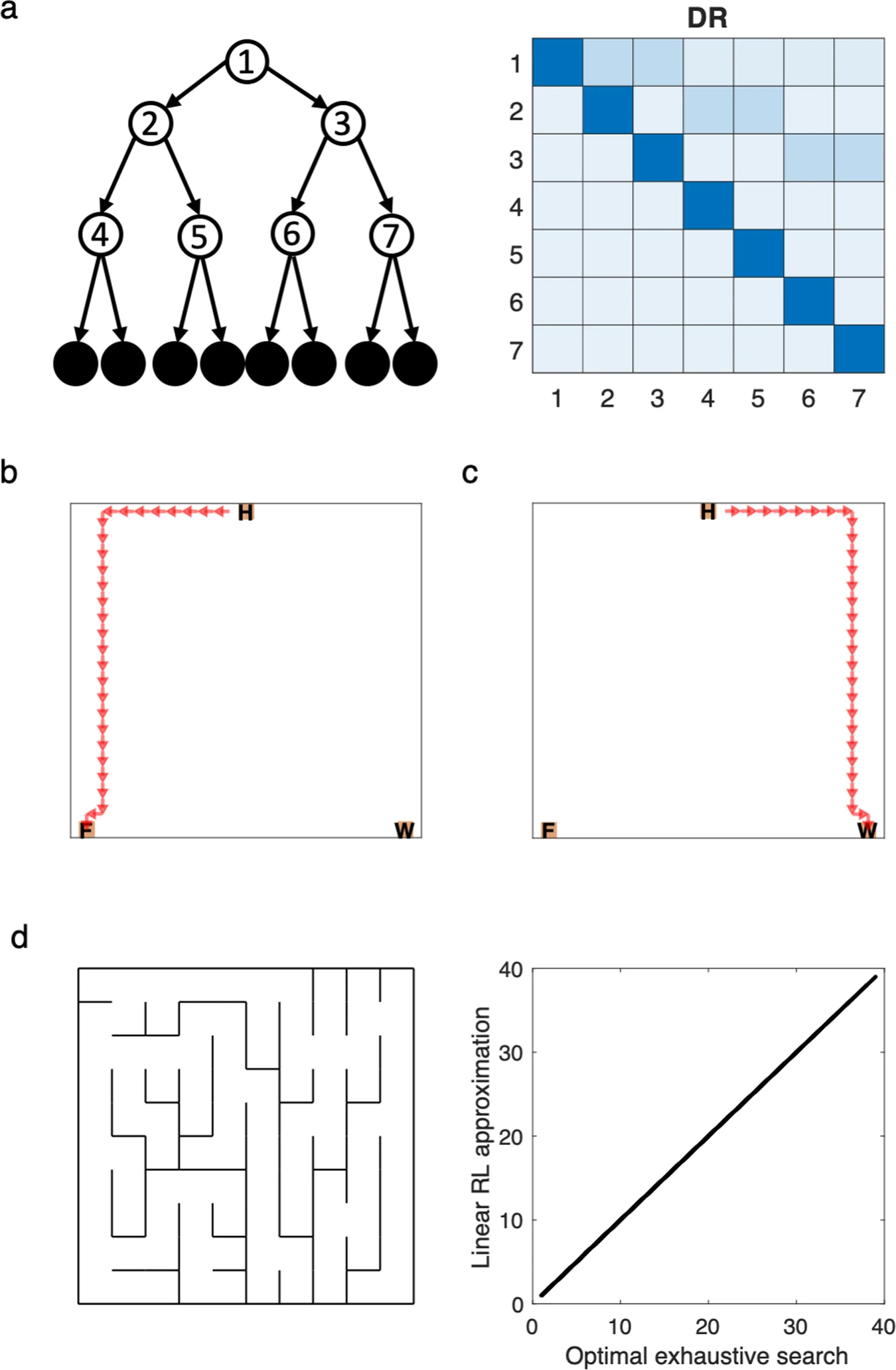
Replanning

이 부분에서는 선형 강화학습(linear RL) 모델이 다양한 재계획(replanning) 과제를 어떻게 해결할 수 있는지를 다룬다. 이 과제들은 주로 보상 또는 목표의 변경(revaluation, devaluation, latent learning) 혹은 전이 구조의 변경(shortcut, detour)을 포함하는데, 이런 변화에 대해 빠르고 효과적으로 행동을 조정할 수 있는 능력은 인간과 동물의 지능적 행동을 평가하는 중요한 척도로 간주된다.

일반적으로 인간과 동물은 이러한 환경 변화에 대해 학습 없이도 즉각적으로 반응할 수 있다. 이러한 능력을 재현하려면 알고리즘적으로 효율적인 지식 전이(transfer) 메커니즘이 필요하다. 기존의 모델 프리(model-free) 강화학습 알고리즘은 보상이 바뀐 경로를 직접 경험해야만 그 보상 정보를 반영해 정책을 수정할 수 있기 때문에, 이러한 재계획 과제를 제대로 해결하지 못한다.

논문에서는 선형 RL 모델이 보상 재평가와 같은 과제를 어떻게 해결하는지를 보여준다. 핵심은, 선형 RL이 사용하는 기본 표현(default representation, DR)은 훈련 시점에 계산되며, 이후에는 보상이 바뀌더라도 이 DR을 그대로 사용할 수 있다는 것이다. 이는 수식적으로 보상 벡터 $\mathbf{r}$만 수정하고 DR을 곱하는 것만으로 새로운 가치 함수를 계산할 수 있음을 의미한다. 즉, 구조 $M$는 유지되면서, 새로운 보상으로 업데이트된 정책을 빠르게 계산할 수 있는 것이다.

예를 들어 Tolman의 잠재 학습(latent learning) 과제를 보면, 쥐는 처음에는 두 개의 보상 구역이 있는 미로를 탐색하게 된다. 이후 그 중 하나의 보상 구역에서 전기 충격을 받게 되는데, 쥐는 해당 경로를 다시 경험하지 않고도 그 경로를 피할 수 있었다. 이는 미리 학습된 DR이 새로운 보상 정보에 따라 즉시 업데이트되어 새로운 정책을 유도할 수 있기 때문이다.

figure 3. Linear RL can explain flexible replanning. a–c Performance of linear RL on a version of Tolman’s latent learning task (a). We simulated the model in a maze representing this task (b) and plotted the probability of choosing each end-box during the training and test phases. The model correctly (c) reallocates choices away from the devalued option. d, e Performance of linear RL in another reward revaluation task5,6, termed policy revaluation (d). Choices from state 1: during the training phase, the model prefers to go to state 3 rather than state 2. Revaluation of the bottom level state reverses this preference (e) similar to human subjects6. f–h Performance of the model in Tolman’s detour task. The structure of the environment changes in this task due to the barrier placed into the maze (g), which blocks the straight path. The model is able to compute the optimized policy using the old DR (following a single, inexpensive update to it) and correctly choose the left path in the test phase (h).

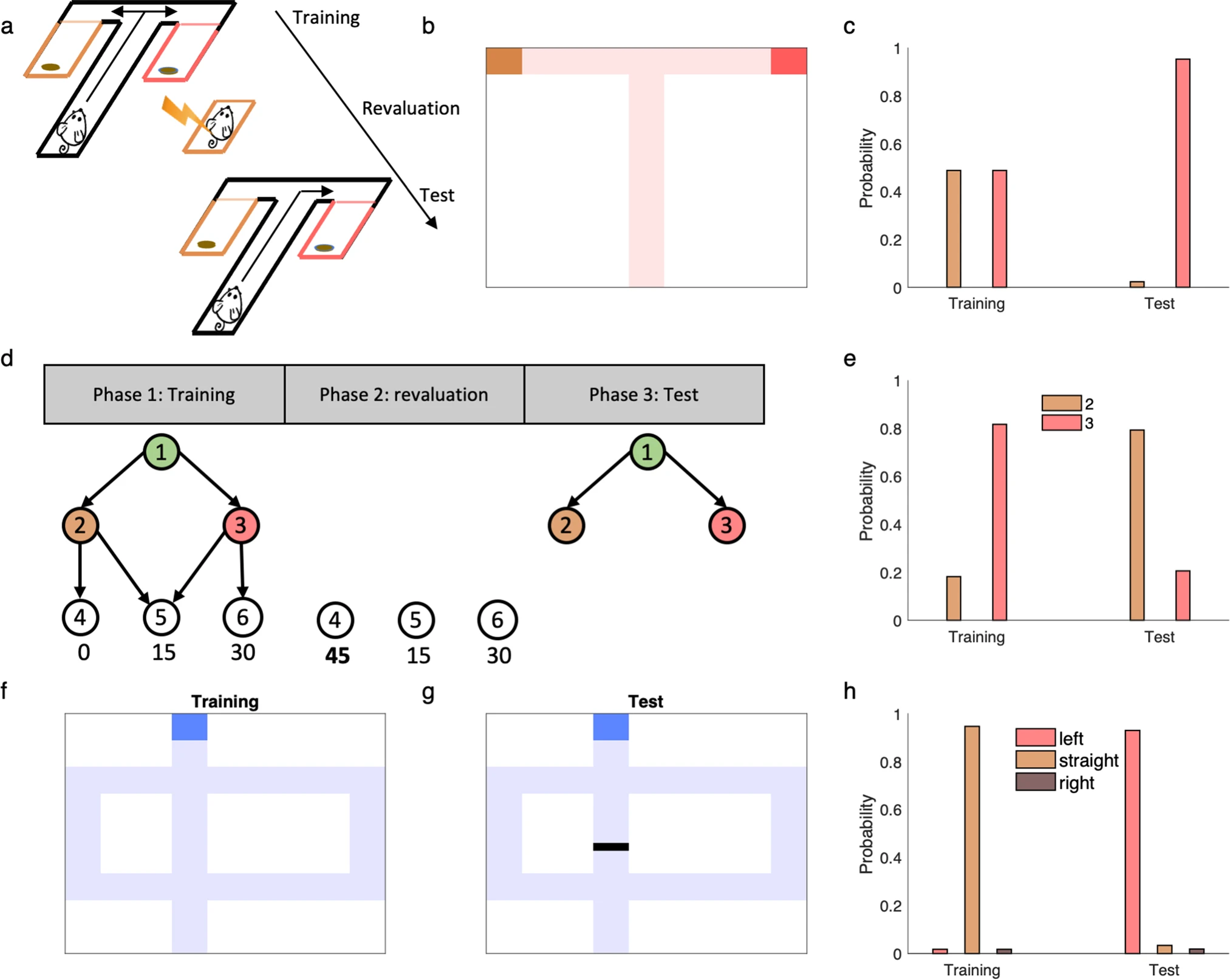
SR(Successor Representation)도 보상 재평가와 같은 단일 단계 과제에서는 작동할 수 있다. 하지만 Russek et al.과 Momennejad et al.이 제안한 정책 재평가(policy revaluation) 과제처럼 여러 단계에 걸친 의사결정이 필요한 경우에는 SR의 한계가 드러난다.

figure 3d의 policy revaluation 과제에서 피험자들은 세 단계를 거쳐 하나의 말단 상태(terminal state)에 도달하게 되는데, 훈련 이후 특정 말단 상태에 높은 보상이 주어지는 구조로 바뀐다. 이 경우, 피험자는 과거에 경험하지 않았던 경로를 선택해야 최적의 보상을 얻을 수 있다. 그러나 SR은 과거 정책에 기반한 상태 전이 예측만을 저장하므로, 새롭게 등장한 보상 경로를 고려하지 못하고 부정확한 정책을 산출하게 된다.

반면 선형 RL은 기본 정책 $\pi_d$에 대한 의존성이 약하고, DR은 다양한 정책 변화에도 안정적이므로, 이러한 과제에서도 새로운 보상 구조에 맞춘 최적 정책을 계산할 수 있다. DR은 여러 가지 기본 정책(예: uniform, 과거에 최적화된 정책 등)을 바탕으로 구성될 수 있으며, 그 자체로도 유용한 정책 업데이트를 가능하게 한다.

다음으로는 환경의 전이 구조(transition structure) 자체가 변화하는 재계획(replanning) 과제—예를 들어 미로에 장벽(barrier)을 추가하여 이전에 선호되던 경로를 차단하는 경우—에 대해 선형 강화학습(linear RL) 모델이 어떻게 대응하는지를 설명한다. 이러한 변화는 환경의 상태 전이 그래프를 변경하게 되며, 이는 SR(successor representation)의 $S_\pi$ 행렬이나 DR(default representation)의 $M$ 행렬이 기존 전이 구조에 기반해 학습되었기 때문에, 이 변화가 반영되지 않으면 정확한 재계획이 불가능하다.

하지만 실험적으로는 인간과 동물이 이러한 전이 구조 변경에도 빠르게 적응하는 능력을 보이며, 이는 기존 강화학습 모델로 설명하기 어렵다. 이를 해결하기 위해, 저자들은 선형 RL을 확장하여 환경 구조 변경에 따른 효율적인 DR 업데이트 방법을 제안한다. 핵심 아이디어는 행렬 항등식(matrix identity)을 이용하여 기존의 DR, 즉 $M_{\text{old}}$에 새로운 변화만 반영한 저차원(low-rank) 행렬 $M_B$를 덧붙이는 방식이다:

\[M = M_{\text{old}} + M_B\]

여기서 $M_B$는 환경의 전이 구조가 변한 상태들에 대해서만 정의되며, 그 rank는 전이가 변경된 상태의 수에 비례한다. 이 방식은 전체 DR을 처음부터 다시 계산하는 것보다 훨씬 효율적이며, 이전에 학습한 DR 구조를 최대한 보존하면서 필요한 수정만 적용할 수 있다. 이를 통해 바뀐 환경에 대해 최적의 가치 함수와 정책을 빠르게 재계산할 수 있다(Fig. 3h).

흥미롭게도 SR 또한 이와 유사한 방식으로 $S_\pi$를 업데이트할 수 있지만, SR은 정책 $\pi$에 의존적이기 때문에 새로운 문제 상황에서 정확한 재계획을 위해서는 정책 자체도 재학습이 필요하다. 반면 DR은 기본 정책 $\pi_d$에 독립적으로 설계되어 있어, 한 번의 간단한 행렬 연산으로 재계획이 가능하다는 점에서 중요한 장점을 갖는다.

Grid fields

기존 이론들은 grid cell이 공간적 또는 추상적인 상태 공간에서의 주기적 관계를 표현하고, 장기적인 계획(planning)이나 탐색(navigation)에 핵심적인 역할을 한다고 주장해왔다. 그러나 grid cell의 계산적 기능이 구체적으로 무엇인지, 그리고 그것이 어떻게 유연한 계획(flexible planning)을 가능하게 하는지에 대해서는 명확하지 않았다.

기존의 고전적 강화학습 이론에서 가치 함수 \(v^*(s)\)를 계산하려면, 현재 상태에서 출발하여 가능한 모든 미래 행동을 고려해야 하며, 이 과정은 매우 비효율적이다. 이를 해결하기 위한 아이디어 중 하나는 단기 전이 정보(예: \(P(s_{t+1}\mid s_t, a_t)\))뿐 아니라, 장기적인 전이 구조(long-range transition structure)를 반영하는 지도 형태의 표현을 사용하는 것이다. SR(successor representation) 모델은 이런 목적을 위해 개발되었으며, 특정 정책 $\pi$ 하에서 미래 상태 방문 기대치를 행렬 $S^\pi$로 저장한다. 이 SR의 고유벡터는 그래프 라플라시안의 고유벡터(eigenvectors of the graph Laplacian)와 동일하며, 이는 주기적이며 grid field와 유사한 공간적 주파수 기반 함수들을 제공한다. 이들 고유함수는 상태 공간 전체에 걸쳐 값 함수나 상태 방문 예측 등을 빠르게 근사할 수 있는 기저 함수(basis functions)로 해석된다.

하지만 SR에는 중요한 한계가 있다. 핵심 문제는 SR이 특정 정책 $\pi$에 따라 구축된다는 점에서 비롯된다. 최적 가치 함수의 벨만 방정식(Eq. (2))에는 각 단계에서의 “max” 연산이 포함되어 있어, 선택된 행동이 후속 상태로의 전이를 결정하며, 이로 인해 장거리 상태 간 전이 지도(long-range transition map)는 정책과 목표에 따라 달라지게 된다. 다시 말해, 목표가 바뀌면 최적 행동도 바뀌고, 그에 따라 후속 상태의 경험 분포 역시 달라져 순수한 공간 구조로서의 안정성이 무너진다.

이러한 구조에서는 고정된 정책 $\pi$를 기준으로 만든 고유벡터 기반의 표현(예: SR의 고유벡터)이 새로운 과제로의 전이에 있어서 제한적인 유용성만을 가지게 된다. 이에 따라 컴퓨터 과학에서는 “representation policy iteration”과 같은 알고리즘이 등장했는데, 이는 각 새로운 과제를 학습할 때마다 정책과 값 함수의 변화에 맞춰 고유벡터 기반 표현을 반복적으로 갱신하는 방식이다. 하지만 이런 반복적인 갱신 방식이 단발(one-shot) 전이 학습에 실제로 효과적인가에 대해서는 여전히 의문이 제기된다.

이에 반해 선형 RL에서 제안된 DR(default representation)은 이러한 단점을 보완한다. DR은 SR과 유사한 구조를 가지면서도, 기본 정책 $\pi_d$에 대해서만 고정되어 있고, 새로운 목표에 대해서도 그대로 사용할 수 있다. 선형 RL에서는 가치 함수가 다음과 같이 계산된다:

\[\exp(v^*) = M P \exp(r)\]

여기서 $M$은 DR로, SR과 유사하지만 정책에 덜 민감하며, 다양한 목표 보상 $r$에 대해 안정적으로 값을 계산할 수 있다. 이것은 grid cell이 실제로 나타내는 것이 DR의 고유벡터일 가능성을 제시한다. 즉, grid cell의 firing pattern은 SR이 아니라 DR의 고유벡터에 해당하는 주기적 함수라는 주장이다. 이 가설은 여러 실험적 결과와 부합한다.

figure 4. The DR as a model of grid fields. a, b Grid fields are sensitive to the geometry of the environment, but are stable with respect to behavior (adapted with permission from Derdikman et al.30). Derdikman and colleagues tested grid fields in a hairpin maze formed by actual barriers, and compared them to those recorded in a “virtual” hairpin maze, in which rats were trained to show hairpin-like behavior in an open field without constraining side walls. Grid fields in the virtual hairpin differ from those in the hairpin maze but are similar to the open field. b This similarity is quantified by the correlation between grid fields in a baseline from an initial open field test and those from the three tasks (hairpin maze, virtual hairpin, the second control open field). This plot is adapted from Derdikman et al.30. Error bars are standard error of the mean. c Grid fields are sensitive to the presence of the home cage only insofar as it introduces new barriers in space, but not through the changes it produces in behavior (Adapted from Sanguinetti-Scheck and Brecht31 licensed under CC BY 4.0). In particular, introducing a plain box (the same shape as the home cage) affects grid fields compared to the open field (left); but substuting the home cage for the box (right) does not further affect the grid code, although it changes behavior. The maps show the correlation between grid fields in the two scenarios. d All eigenvectors of the DR are independent from behavioral policies and periodic, similar to grid fields. Three example eigenvectors from a 50 × 50 maze are plotted. See Supplementary Fig. 1 for other eigenvectors. Source data are provided as a Source Data file.

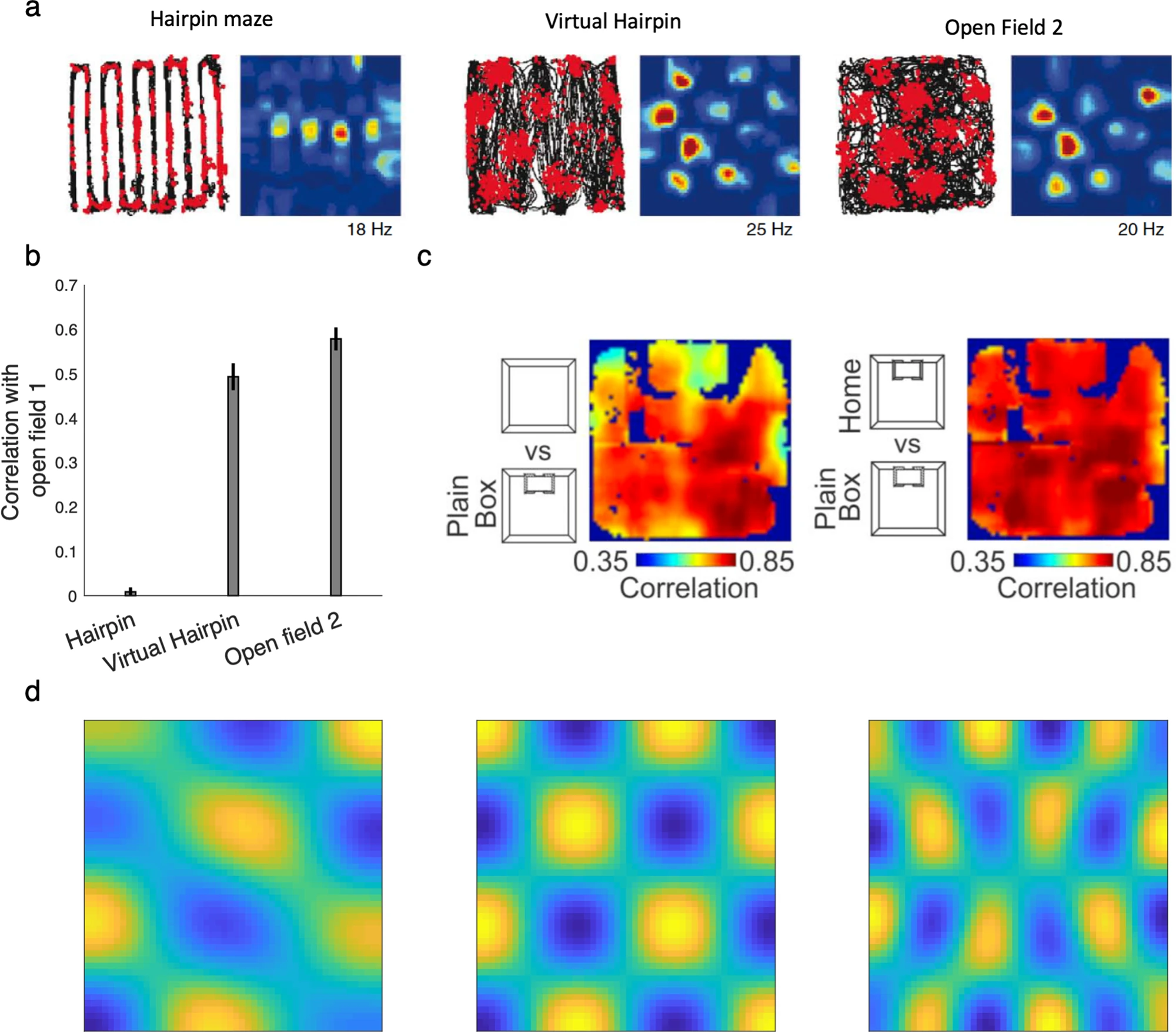
이러한 주장을 뒷받침하는 실험적 증거는 Figure 4에 제시되어 있다. Figure 4a–b에서는 벽을 세워 hairpin maze를 만들었을 때 grid field가 변화하지만, 벽 없이 동일한 행동 경로를 학습한 경우 grid field에는 변화가 없었다. 이는 정책 변화는 grid field에 영향을 주지 않으며, 오직 환경의 전이 구조(transition structure)만이 영향을 미친다는 것을 시사한다. Figure 4c는 벽의 형태가 동물의 집과 동일할 때 grid field가 반응하지만, 그것이 실제 집인지 여부는 중요하지 않다는 것을 보여주며, grid cell이 객관적인 환경 구조에 더 민감하다는 점을 강조한다. Figure 4d는 DR의 고유벡터가 2D 공간에서 주기적인 grid-like 패턴을 형성한다는 것을 시각적으로 보여준다. 이는 grid cell이 DR의 고유벡터를 바탕으로 공간 구조를 표현한다는 주장을 뒷받침한다.

이러한 결과는 기존 SR 기반 모델들이 가지는 정책 의존성과 그에 따른 불안정성 문제를 해결할 수 있으며, grid field가 다양한 목표와 행동 전략 변화 속에서도 정상적으로 유지될 수 있는 계산 기제로서 DR의 역할을 정당화해준다. 더불어 DR은 경로상의 지역적 비용(local cost)도 반영할 수 있기 때문에, 험한 지형이나 장애물과 같은 환경적 특성에 따라 grid field의 강도나 구조가 달라질 수 있다는 예측도 가능하게 한다.

마지막으로 DR은 경로상의 지역적 비용(local cost)도 고려한다는 점에서 SR보다 더 현실적이다. 이로 인해 지형의 난이도(예: 경사진 지형, 험지 등)가 grid cell의 반응에 영향을 미칠 수 있다는 예측도 가능하다.

Border cells

이 문단은 entorhinal cortex의 border cells가 선형 강화학습(linear RL) 프레임워크 내에서 어떤 계산적 역할을 가질 수 있는지 설명한다. 앞서 설명된 것처럼, 환경 내 장애물(barriers)과 같은 변화는 기본 전이 구조를 변경시켜 DR(Default Representation)을 갱신해야 한다. Tolman의 detour task(Fig. 3f–h)를 통해 이 문제를 다룰 때, 저자들은 전체 DR을 재계산하지 않고, 원래의 DR에 저랭크(low-rank) 보정 행렬 $M_B$를 더하는 방식으로 새로운 DR을 표현했다. 이 방식은 공간 거리 맵(DR)을 여러 구성 요소(component)들의 합으로 표현할 수 있는 구조적 가능성을 제시한다.

figure 5. The model explains border cells. a Rate maps for a representative border cell in different boxes; adapted from Solstad et al.41 with permission from AAAS. b Columns of the matrix required to update the DR matrix to account for the wall resemble border cells. Four example columns from a 20 × 20 maze are plotted. See also Supplementary Fig. 2. Source data are provided as a Source Data file.

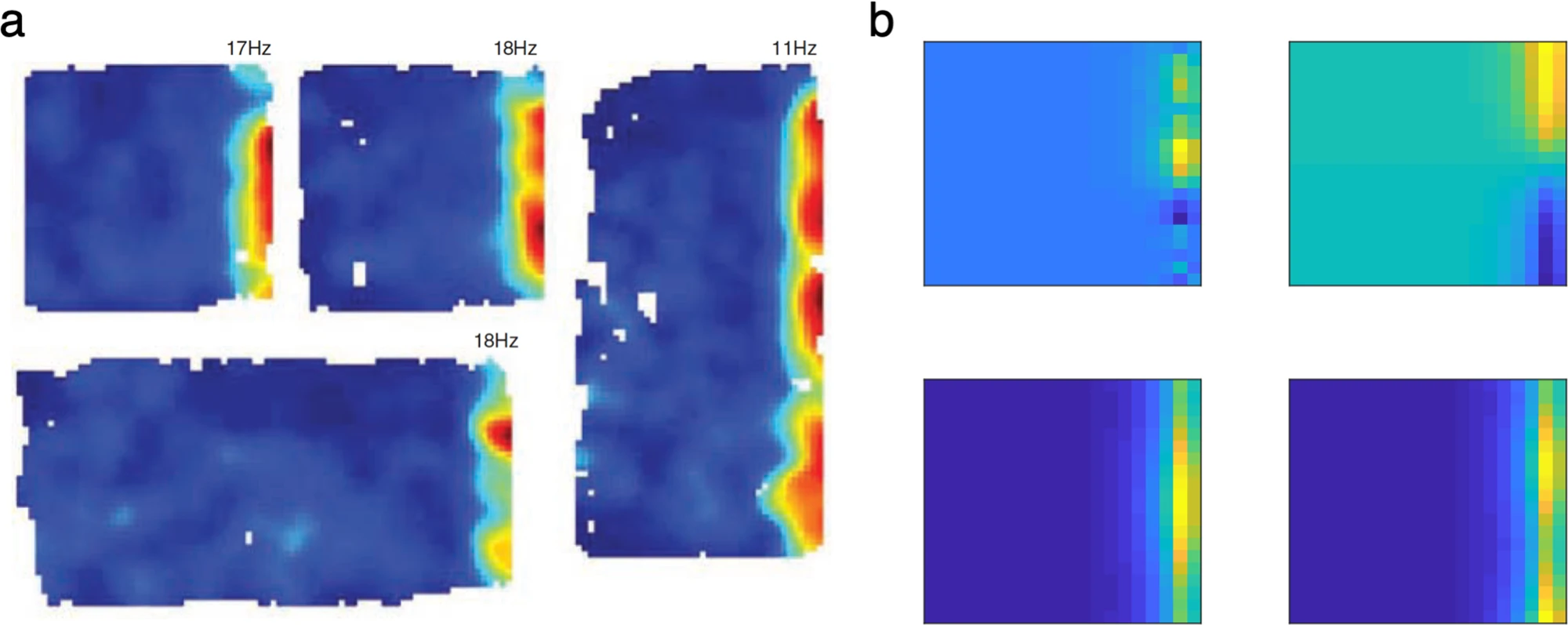
이 맥락에서 entorhinal border cells는 중요한 계산적 단서로 제시된다(Fig. 5a). 이 세포들은 동물이 환경의 경계 근처에 있을 때만 강하게 반응하며, 환경 구조가 바뀌어도 이러한 경계 민감성은 유지된다. 흥미롭게도, DR의 보정 행렬 $M_B$의 열벡터는 border cells의 활성 패턴과 유사한 특성을 보인다(Fig. 5b). 즉, 이들은 기존 DR의 저차원(eigenvector 기반) 표현과 함께 지도(map)를 구성하는 또 다른 기저 함수(basis function)로 해석될 수 있으며, grid cells와 함께 공통된 표현 체계로 통합될 수 있다.

이러한 구조는 DR을 장애물과 같은 환경적 특징의 조합으로 나타내는 두 가지 방식을 함의한다. 첫째는 $M_B$를 별도의 가산 요소로 유지하는 방식(예: border cells로 표현), 둘째는 기존 맵(예: grid cells, $M_{old}$) 자체를 업데이트하여 변경사항을 통합하는 방식이다. 두 번째 방식은 grid cells의 공간적 주기성이 장애물에 의해 변할 수 있음을 시사하며, 첫 번째 방식은 장애물이 grid map에 영향을 주지 않음을 시사한다. 실험적으로는 grid cells 중 일부는 장애물에 민감하게 반응하고, 일부는 반응하지 않으며, 이러한 차이는 환경에서의 학습 정도에 따라 달라질 수 있음이 보고되었다. 따라서 DR의 보정 항 $M_B$는 초기에는 별도로 표현되지만, 환경이 안정적이라면 이후 전체 맵에 통합될 수 있다는 가능성이 제시된다.

Planning in environments with stochastic transitions

이 문단은 선형 강화학습(linear RL) 모델이 확률적 전이(stochastic transitions)를 가지는 환경에서 어떻게 확장될 수 있는지를 다룬다. 기존 논의는 결정론적 환경(deterministic environments), 예를 들어 미로처럼 특정 행동이 항상 동일한 다음 상태를 유도하는 구조에 초점을 맞췄다. 이 경우 정책(policy)은 상태 전이 확률의 연속적이고 미분 가능한 공간에서 최적화될 수 있기 때문에 linear RL의 장점이 잘 발휘된다. 그러나 생물학적으로 중요한 많은 환경은 전이 자체가 확률적이다. 저자들은 이러한 환경에도 linear RL을 적용할 수 있는 방법으로, 먼저 해당 환경을 완전하게 제어 가능한 결정론적 환경으로 근사하여 최적 전이 행렬을 구하고, 그 후 실제 행동 정책 중 이 전이를 가장 잘 근사하는 정책을 선택하는 절차를 제안한다. 이때 두 번째 단계는 일종의 투영(projection)으로, 자세한 방법은 부록(Methods)에서 설명된다.

figure 6. Linear RL in environments with stochastic transitions. a The two-step Markov decision task, in which first-stage actions A1 and A2 stochastically transition to second-stage states. b Linear RL solves this task similar to classical model-based learning, such that the effect of reward (vs nonreward) on the subsequent first-stage choice (stay or switch, with respect to that on the current trial) depends on the type of transition (common: 70%; rare: 30%). c A task with stochastic transitions that linear RL fails to solve. Here, taking A1 and A2 at S1 deterministically leads to S2 and S3, respectively. However, taking either of A1 and A2 in state S2 stochastically leads to two different states with 10 and –10 reward (with 50–50% chance). Therefore, expected value of state S3 is higher than that of S2, and A2 is the optimal action in S1. Linear RL incorrectly chooses A1 in S1, however.

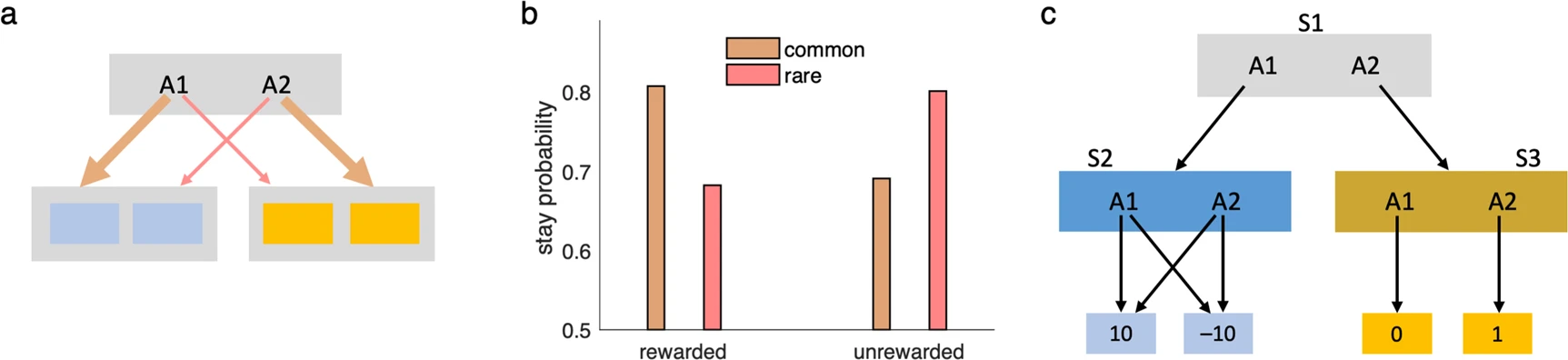
이 접근 방식의 대표적인 예로 저자들은 two-step MDP 과제를 소개한다(Fig. 6a). 이 과제는 심리학과 신경과학에서 모델 기반(model-based) 학습의 존재를 실험적으로 입증하는 데 자주 쓰인다. 첫 번째 상태에서 행동을 선택하면 확률적으로 두 번째 상태 중 하나로 이동하며(0.7의 일반 전이, 0.3의 희귀 전이), 이후 보상을 받게 된다. 실험 참가자는 시간이 지남에 따라 변화하는 보상 확률에 맞춰 정책을 조정해야 하며, 이때 전이 구조에 대한 민감한 행동 변경은 모델 기반 전략의 증거로 해석된다. Linear RL은 확률적 전이를 고려한 확장된 형태로 이 과제에서 실험 참가자와 유사한 전이 민감성 패턴을 재현한다(Fig. 6b).

그러나 이 방식에는 한계가 있다. 전이 확률을 무시하고 완전 제어 가능한 상태로 가정했을 때, 그 오차가 상위 단계의 정책에까지 영향을 주는 경우가 존재한다. 예를 들어 Fig. 6c와 같은 경우, 첫 번째 상태 $S_1$에서 linear RL은 $A_1$을 선호하지만 실제로는 $A_2$가 평균적으로 더 나은 선택이다. 이는 전 단계 $S_2$에서의 전이 구조가 제어 가능하다는 잘못된 가정 하에 overly optimistic한 가치 추정이 발생했기 때문이다. 이런 상황에서 인간은 잘못된 선택을 하거나, 더 복잡하고 반복적인 모델 기반 탐색 전략으로 회귀할 가능성이 있다. 이로 인해 계획 시간이 늘어나는 행동 패턴이 관찰될 수 있으며, 이는 linear RL 모델의 예측이다. 하지만 이러한 예측은 현재까지 실험적으로 검증되지 않았다.

Habits and inflexible behavior

inear RL에서 default policy는 행동 선택에 대한 부드러운 사전 가정(soft prior assumptions)을 제공한다. 이는 미래의 최적 선택 경로를 예측하는 문제를 보다 효율적이면서 근사적으로 해결하는 데 도움을 준다. 지금까지 시뮬레이션에서는 이 default policy를 균등 분포(uniform over successors)로 설정했는데, 이는 알고리즘이 기본 정책에 민감하지 않다는 성질 덕분에 잘 작동했다. 그러나 이러한 민감도 부족은 반대로 비균등(non-uniform) 또는 경험을 통해 학습된 default policy를 사용할 수도 있게 한다.

특정 행동 선택 경향이 안정적으로 반복되는 상황에서는, 그 경향을 반영한 default policy가 더 좋은 근사치가 될 수 있다. 이 경우 linear RL은 해당 정책에 따라 일관된 편향된 행동을 유도하게 되며, 이로 인해 인간 행동에서 자주 나타나는 습관적인 선택(habit), Stroop 효과, Pavlovian 편향 등을 자연스럽게 설명할 수 있다. 즉, 이러한 행동은 단순히 잘못된 선택이 아니라, 효율적인 계획을 위한 시스템적 선택 편향으로 해석할 수 있다.

또한 기존 논의에서는 default policy가 고정되어 있다고 가정했지만, 이 모델은 경험 기반으로 default policy가 점진적으로 학습되는 형태로 확장할 수 있다. 이를 위해 저자들은 작은 학습률을 가진 델타 규칙(delta rule) 기반의 업데이트 방식을 사용했다. 이때 default policy의 갱신이 있을 때마다 전체 DR(기본 표현) 행렬을 새로 계산할 필요는 없으며, 이전 섹션에서 설명한 행렬 역행렬 항등식(matrix inversion identity)을 활용해 효율적으로 업데이트할 수 있다.

기본적으로 default policy는 초기에는 균등하거나 비편향적일 수 있지만, 오랜 학습(또는 overtraining)을 통해 특정 행동 패턴에 점차 편향된다. 이 편향된 default policy는 결정 정책에 부드러운 영향(soft bias)을 주어, 기존의 익숙한 행동을 선택할 확률을 높인다. 그 결과, 개별 선택 수준에서는 더 많은 오류(비최적 행동)가 발생할 수 있으며, 전체적인 행동 궤적도 왜곡될 수 있다.

이러한 현상은 모델 내의 control cost와 reward 간의 상대적인 스케일을 조절하는 상수 파라미터에 따라 달라진다. 예를 들어, control cost가 높으면 default policy로부터 벗어나는 행동을 하기 위해 더 큰 비용이 필요하게 되어, 기존 정책을 더 고수하려는 경향이 생긴다.

figure 7. Learning the default policy results in soft habits. a–c A simple choice task (a) in which the default policy has been extensively trained under conditions in which state B is rewarding. In this case, an overtrained default policy favors choice of B by default (b) which softly biases choice away from A even after the rewarded goal has moved in the test phase (c). This effect is larger when the control cost parameter, λ, is larger. This is because this parameter controls the relative weight of the control cost (for diverging from default policy; see “Methods”, Eq. (6)). d The default policy has been trained extensively to find a goal located in the blue square. e, f Performance of the model with overtrained vs. uniform (i.e. no training) default policies on this task, in which the goal has been moved but it is still in the same room (e). The overtrained model performs better here (f). However, when the goal has been moved to a different room (g–i), the model with a uniform default policy (no training; g) performs better than the overtrained model, which habitually enters the room in which it has been overtrained in (h). Mean, standard error of the mean, and distribution of data across 1000 simulations are plotted in panels f and i. For overtraining, the model has experienced 1000 episodes of the task with step-size 0.01. Source data are provided as a Source Data file.

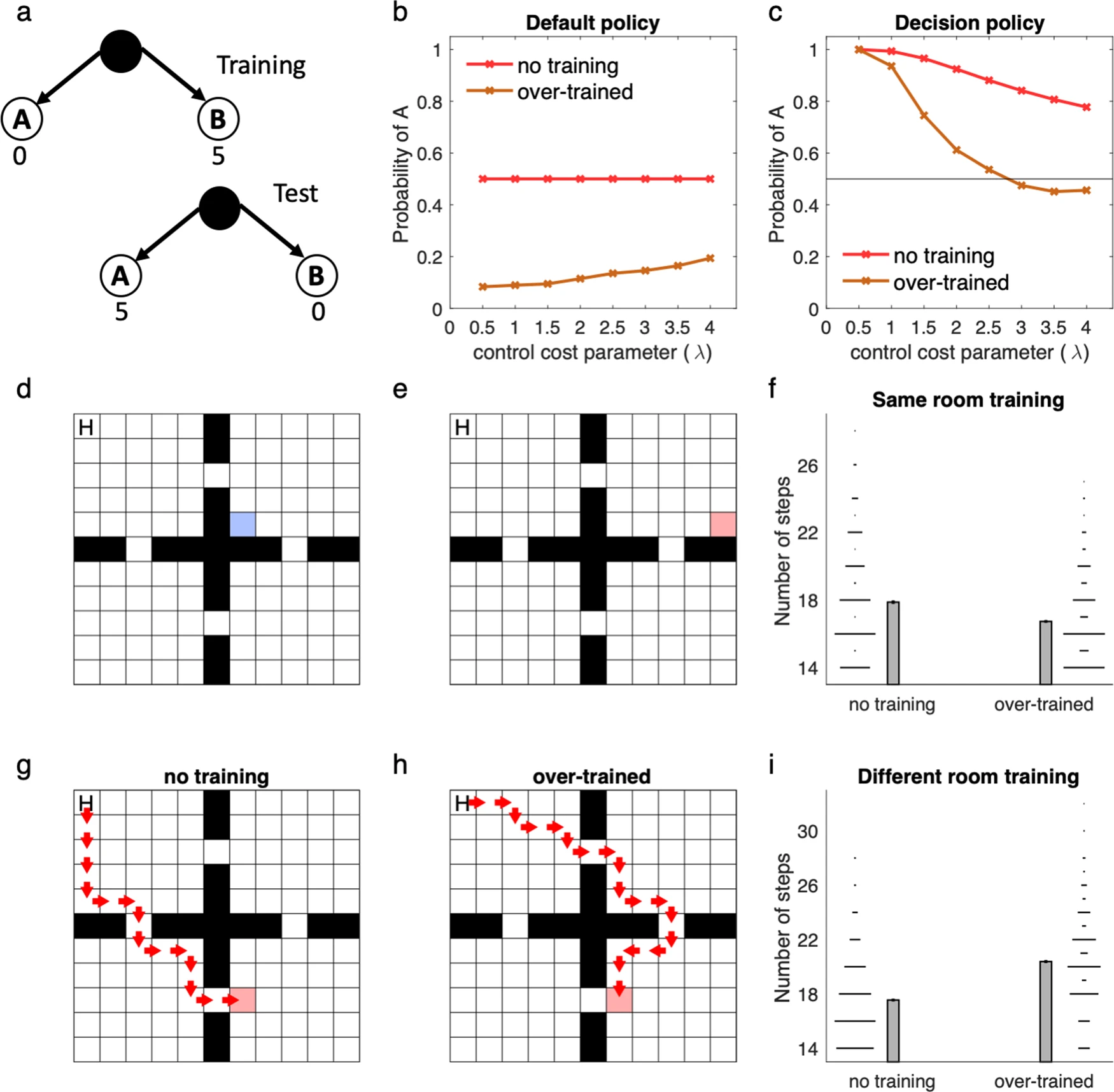
저자들은 이러한 현상이 실제 행동 편향을 어떻게 만들어내는지 네 개의 방으로 구성된 환경(four-room environment)에서 시뮬레이션을 통해 보여준다 (Fig. 7 참조). 초기 학습에서는 목표(goal)가 파란 박스에 위치해 있었고, 이 환경에서 default policy가 훈련되었다(Fig. 7d). 이후 목표의 위치를 다음과 같이 변경하여 실험했다:

• 근접한 위치로 이동한 경우 (같은 방 내에서 이동, Fig. 7e–f): 이때는 이전 정책과 새로운 정책 간의 겹침이 커서, 훈련된 default policy가 도움이 되었다.

• 완전히 다른 방으로 이동한 경우 (다른 방으로 이동, Fig. 7g–i): 이때는 이전 정책과 새 정책 간의 겹침이 거의 없어서, default policy의 편향이 새로운 목표를 향한 경로를 왜곡하고, 서브옵티멀(suboptimal)한 경로를 선택함. 이 경우 모델은 습관적 행동의 특징(habitual signature)을 보이는데, 이는 이전에 목표가 있던 방으로 여전히 들어가려는 경향이다.

즉, linear RL에서 경험 기반으로 학습된 default policy는 때로는 새로운 목표에 빠르게 적응할 수 있게 도와주지만, 환경 변화가 클 경우 오히려 부적절한 일반화와 행동 경직성을 유발할 수 있다는 점을 이 실험은 잘 보여준다.

Cognitive control

인지적 통제는 사람이 자동적인 반응(습관적이거나 흔한 행동) 대신, 내적으로 설정한 목표를 달성하기 위한 행동을 수행하는 능력이다. 예를 들어, Stroop task에서 단어 읽기보다 색깔 이름 말하기가 더 어렵고 오류가 많다는 현상이 대표적인 사례이다.

이러한 현상은 직관적으로는 명확하지만, 이론적으로는 몇 가지 퍼즐을 야기한다. 첫 번째는 왜 어떤 행동이 더 선호되는가이고, 두 번째는 왜 그런 행동을 억제하고 다른 행동을 수행하는 것이 ‘비용(costly)’처럼 느껴지는가 하는 점이다. 이에 대한 기존 설명은 뇌 자원의 경쟁(resource competition)이나 에너지 소모 같은 생물학적 비용을 들고는 했지만, linear RL은 전혀 다른 접근법을 제안한다.

linear RL에서는 행동 선택에 기본 정책(default policy)이라는 것이 있으며, 이 정책에서 벗어난 행동은 KL-divergence에 기반한 control cost를 유발한다. 즉, 덜 익숙하거나 잘 사용되지 않는 행동을 선택할 경우, 보상 함수에서 해당 행동은 실제 보상 외에 추가적인 벌점(penalty)을 받게 되는 구조다. 이 벌점은 계획을 더 효율적으로 수행하기 위한 계산상의 비용이지, 실제 에너지 소비를 반영하는 것이 아니다.

이러한 구조는 기존의 인지 통제를 결정이론적 문제(decision-theoretic problem)로 보려는 연구들과 유사하며, 행동의 보상과 통제 비용 사이의 균형을 통해 행동이 선택된다고 본다. 특히, Figure 8a와 8b에서는 default policy에서 덜 선택되는 행동일수록 control cost가 커지는 양상이 시뮬레이션으로 나타난다. 예컨대 Stroop task에서 ‘색깔 이름 말하기(color naming)’는 default policy에서 낮은 확률을 가지므로 높은 control cost를 가진다. 그 결과, 동일한 보상 조건 하에서는 오류 확률이 증가하게 된다. 이것이 바로 Stroop 효과의 computational한 설명이다.

figure 8. Linear RL captures prepotent actions and costs of cognitive control. a, b The control cost is plotted as a function of the decision policy. For a uniform distribution (a) as the default policy, the control cost is a symmetric function of the decision policy. When the default policy is skewed toward a more likely response (b), the control cost is higher for reliably performing the action that is more unlikely under the default. c People show classical Stroop effect in a color-naming Stroop task in which the name of colors are printed in the same or different color. These errors, however, are reduced in potential reward trials, in which correct response is associated with monetary reward51. d The linear RL model shows the same behavior, because the default probability is larger for the automatic response (i.e. word reading). Promising reward reduces this effect because the agent balances expected reward against the control cost to determine the optimized policy. Data in (c) are adapted from Krebs et al.51, in which mean and standard error of the mean are plotted (obtained over n = 20 independent samples). Source data are provided as a Source Data file.

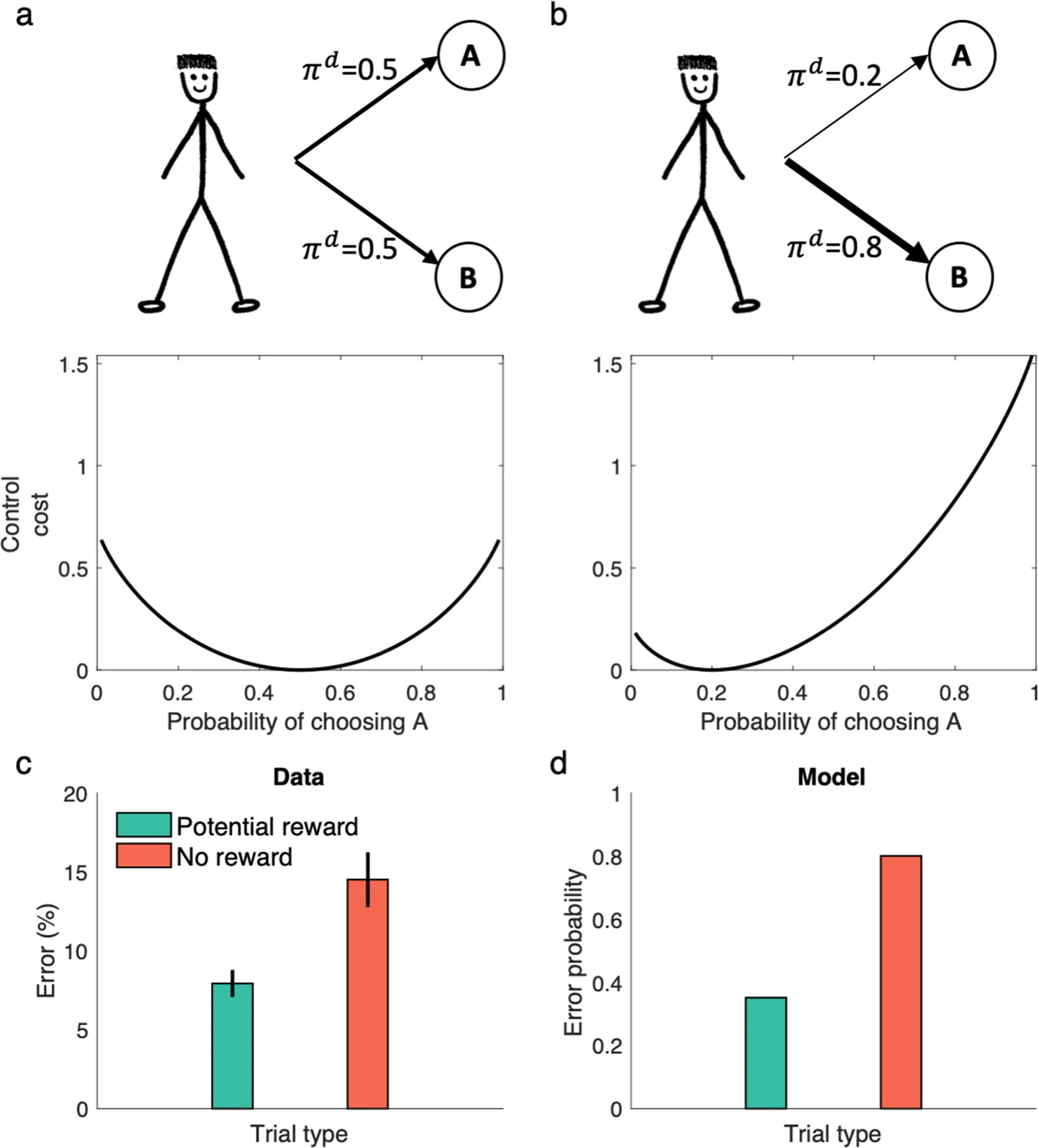
먼저, Figure 8a는 기본 정책(default policy)이 균등 분포일 때의 control cost를 보여준다. 이 경우, 특정 행동을 선택하는 데 드는 통제 비용은 결정 정책의 분포에 대해 대칭적으로 작용한다. 다시 말해, 어떤 행동이든 default로부터 벗어난 정도에 비례하여 동일한 비용이 발생한다.

그러나 Figure 8b는 default policy가 비균등하게 skew되어 있을 경우를 시뮬레이션한 결과를 보여준다. 이 시나리오에서는 어떤 행동(예: Stroop task에서의 ‘color naming’)이 기본적으로 덜 선택되는 행동일 경우, 그것을 선택하는 데 훨씬 높은 통제 비용(control cost)이 든다. 이러한 구조는 실험적으로도 확인된 Stroop 효과를 설명해주며, 왜 사람들이 색깔 이름을 말하는 과제에서 더 많은 오류를 범하는지를 이해할 수 있게 한다.

Figure 8c는 실제 실험 결과를 보여준다. 색 이름을 말하는 Stroop task에서 보상이 주어졌을 때 오류율이 감소한다는 실험(Krebs et al. 51)을 기반으로 한 데이터이다. 이는 사람들이 단순히 자동 반응에 따라 행동하지 않고, 보상의 기대값이 높아지면 더 어렵고 effortful한 행동도 잘 수행할 수 있음을 시사한다.

Figure 8d는 이러한 현상을 linear RL 모델이 동일하게 재현해낼 수 있음을 보여준다. 보상이 높아질수록, model은 기대 보상(expected reward)과 control cost를 균형 있게 고려하여 최적 정책을 결정하기 때문에, 어려운 행동(예: color naming)도 더 자주 선택하게 된다. 이는 보상에 의해 인지적 통제가 가능함을 computational하게 설명해주는 사례이다.

하지만 이 모델은 이러한 오류가 필연적인 것이 아님을도 보여준다. 만약 ‘색깔 이름 말하기’에 정확한 수행에 대한 보상을 증가시키면, 이 행동이 얻는 총 기대 보상이 커져 control cost를 상쇄할 수 있다. Figure 8c와 8d는 실제 보상이 증가할 때 Stroop 오류가 감소하는 패턴을 보여준다. 이는 실험적으로도 관찰된 바 있는 결과이며, 보상이 높은 경우 어려운 과제도 더 잘 수행될 수 있음을 예측한다.

Pavlovian-instrumental transfer

Pavlovian-instrumental transfer (PIT)는 행동 선택에서 발생하는 비합리적인 편향 중 하나로, linear RL 모델이 이를 어떻게 설명할 수 있는지를 보여준다. PIT는 생물이 특정 자극(예: 종소리)과 보상(예: 음식) 사이의 파블로프식 연합을 형성한 이후, 그 자극이 이후의 행동 선택(예: 레버 누르기)에 영향을 주는 현상이다. 주목할 점은, 이 자극은 실제로 행동-보상 연합과는 무관함에도 불구하고, 행동 선택에 영향을 준다는 것이다. 이로 인해 기존의 강화학습(RL) 모델이나 SR(successor representation) 모델은 PIT 현상을 제대로 설명하지 못한다. 전통적인 모델들은 자극이 행동-결과 간의 관계를 바꾸지 않기 때문에, 행동 선택에 영향을 주지 않아야 한다고 예측하기 때문이다.

하지만 linear RL 모델은 기본 정책(default policy)의 개념을 통해 이 현상을 자연스럽게 설명한다. 파블로프식 학습 단계에서, 특정 자극(예: Stimulus 1)이 보상과 함께 나타나는 빈도가 높아지면, 이 자극이 주어진 상태에서 해당 보상이 더 자주 발생한다는 default 정책 기반의 기대가 형성된다. 이후 PIT 테스트 단계에서는, 자극이 등장함으로써 기본 정책이 특정 보상을 예측하고, 그 보상과 연합된 행동을 선택하는 쪽으로 편향된 결정 정책을 유도하게 된다.

figure 9. Linear RL explains Pavlovian-instrumental transfer. a the task testing outcome-specific PIT consists of three phases: a Pavlovian training phase, an instrumental training phase, and the PIT test. Outcomes 1 and 2 are both rewarding. During PIT test, both stimuli are presented in succession, and “same” responses denote the one whose associated outcome matches that associated with the presented stimulus, e.g. Response 1 chosen following presentation of Stimulus 1. The other response is “different.” b, c Data adapted from Corbit et al.84 when rats are hungry (b) and simulated behavior of the model (c). The model learns the default policy during the Pavlovian phase, which biases performance during the PIT test. d, e Outcome-specific PIT persists even when rats are sated on both outcomes (d). The model shows the same behavior (e) because default state probabilities learned during Pavlovian training influence responses even in the absence of reward. Mean and standard error of the mean are plotted in b and d. Data in b and d are adapted from Corbit et al.84, in which the mean and standard error of the mean are plotted (obtained over n = 16 independent samples). Source data are provided as a Source Data file.

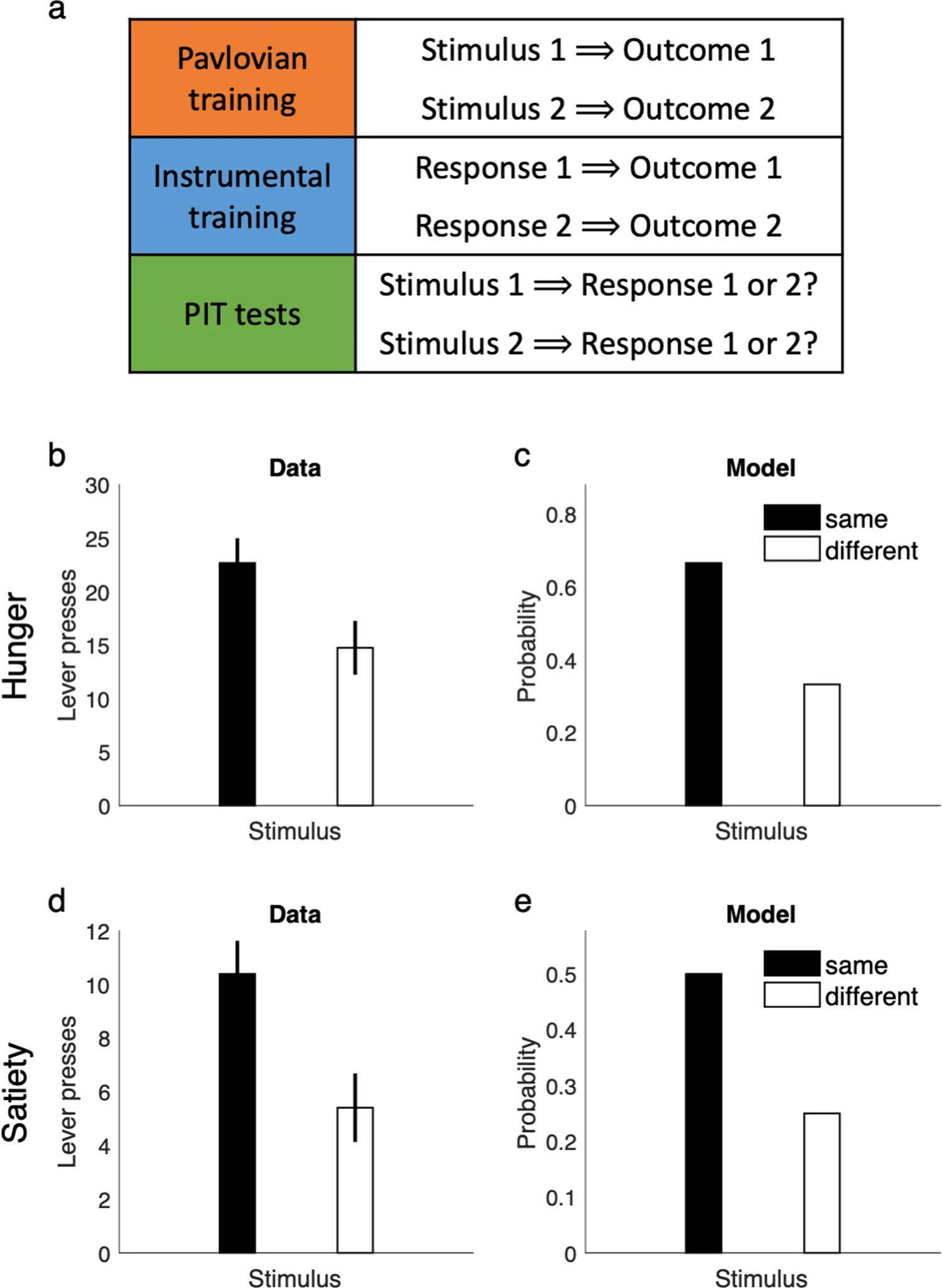
Figure 9a는 PIT 과제의 전체 실험 절차를 도식화한 것이다. 실험은 세 단계로 구성된다. 첫 번째는 Pavlovian 학습 단계로, 이 단계에서 동물은 특정 자극(예: 빛, Stimulus 1)이 특정 보상(Outcome 1)을 예측함을 학습한다. 두 번째는 도구적 학습 단계로, 여기서는 동물이 레버를 눌러서 동일한 보상을 얻는 법을 배운다. 세 번째는 PIT 테스트 단계로, 자극이 제시되면 동물은 해당 자극과 연합된 보상을 얻는 데 효과적인 행동을 더 많이 선택하게 된다. 중요한 점은, 자극이 실제 행동 결과에는 아무런 영향을 미치지 않음에도 불구하고 행동이 편향된다는 것이다.

Figure 9b는 이 실험을 실제 동물(쥐)에게 시행했을 때 나타난 결과를 보여준다. 쥐가 배고픈 상태에서 PIT 테스트를 수행하면, 자극이 제시되었을 때 해당 자극과 연합된 보상을 목표로 하는 행동을 유의미하게 더 많이 수행함을 보여준다. 즉, 자극이 도구적 행동 선택에 영향을 미친다는 것이다.

Figure 9c는 linear RL 모델이 동일한 실험 조건에서 PIT 편향을 어떻게 재현하는지를 보여준다. 모델은 Pavlovian 학습 단계에서 기본 정책(default policy)을 학습하고, 이 기본 정책은 특정 자극이 특정 보상 상태를 더 자주 야기한다고 내면화한다. 이후 테스트 단계에서는 보상이 없거나 자극이 행동 결과에 직접 영향을 주지 않아도, 기본 정책의 영향으로 관련 행동이 더 빈번히 선택된다. 이는 실험 결과와 일치하는 패턴을 보여준다.

Figure 9d는 흥미로운 확장 실험으로, 동물이 포만 상태(보상에 대한 동기가 약화된 상태)에서도 PIT 효과가 유지됨을 보여준다. 이는 단순히 보상의 유무나 가치 때문이 아니라, 자극이 상태 기대에 영향을 주기 때문에 발생한다는 점을 강조한다.

Figure 9e는 위 실험을 linear RL 모델로 시뮬레이션한 결과로, 실제 실험과 동일하게 포만 상태에서도 PIT 편향이 유지됨을 보여준다. 이는 모델이 보상 신호가 아닌, 감각적 상태 특징을 반영한 기본 정책을 통해 행동을 설명할 수 있다는 강점을 보여준다.

전반적으로 PIT가 단순히 보상 기반이 아니라, 자극에 기반한 상태 기대가 행동 선택을 편향시킨다는 사실을 보여주며, linear RL이 이러한 편향을 기본 정책을 통한 연산으로 자연스럽게 설명할 수 있음을 시각적으로 입증한다.

Discussion

논문의 결론 부분은 매우 길고 복잡하지만, 중심 주제를 기준으로 다음과 같은 하위 내용으로 나눌 수 있다:

문제의 핵심과 linear RL 도입

기존 강화학습 모델들이 유연한 계획(plan)과 경로 재계산(replanning)을 충분히 설명하지 못했던 문제를 지적하며, 이를 해결하기 위한 새로운 접근법으로서 linear RL 모델을 제안한다. 이 모델은 default policy를 기준으로 한 soft한 최적화를 통해 interdependent policy 문제를 완화하고, 이를 통해 안정적이고 효율적인 의사결정이 가능하다고 주장한다.

DR과 SR의 비교 및 장점

DR(default representation)은 SR(successor representation)과 유사하지만, 목표(goal)가 바뀌더라도 안정적으로 재사용할 수 있는 특성을 가진다. 이는 유연한 재계산과 재사용을 가능하게 하며, grid cell의 안정성과도 잘 들어맞는다고 설명한다.

뇌 내 인지 지도와 grid/border cell의 역할

DR은 entorhinal cortex 내 grid cell이 가지는 안정적이고 정기적인 반응 특성과 연결된다. 또한 DR의 갱신 방식이 border cell의 반응 특성과도 유사함을 보여주며, 이 두 종류의 세포가 인지 지도의 기저 구성 요소(basis functions)로 작용함을 시사한다.

습관과 인지적 비유연성의 설명

linear RL의 default policy는 일종의 편향(bias)을 낳는데, 이는 습관, Stroop 효과, Pavlovian 편향 등과 같은 다양한 인지적 비유연성 현상을 설명할 수 있게 한다. 이러한 편향은 에이전트가 효율적으로 계획하기 위한 절충의 결과물로 이해된다.

인지적 제어(cognitive control) 비용의 정량화

default policy로부터의 편차를 비용(cost)으로 설정한 linear RL은 인지적 제어가 왜 ‘비용이 큰’ 것으로 느껴지는지를 설명할 수 있는 이론적 기반을 제공한다. 예를 들어 Stroop 과제에서의 오류율이나 반응 시간 증가 같은 현상을 수학적으로 설명할 수 있다.

Pavlovian-instrumental transfer (PIT)의 설명

PIT는 기존 강화학습 모델로 설명이 어려운 현상인데, linear RL에서는 default policy의 학습 과정에서 생긴 편향이 행동에 영향을 미치는 방식으로 자연스럽게 설명된다. 이 과정은 보상 자체가 아닌 감각적(state-based) 연합에 의해 작동한다는 점에서, 중독 행동 등과도 연결된다.

미래 연구 방향과 뇌 기반 구현 가능성

linear RL이 제공하는 컴퓨팅 모델은 단순한 행렬-벡터 곱 연산으로 이루어져 있어 신경망으로 구현 가능하며, 다양한 뇌 영역에서 이 계산이 어떻게 분산되어 수행될 수 있는지도 탐구할 여지가 많다. 또한 grid cell의 eigenvector 표현, cost-sensitive planning, Bayesian planning-as-inference 등 다양한 이론과 통합될 수 있는 가능성을 보여준다.

default policy의 학습과 최적성 문제

어떤 default policy를 설정해야 최적의 성능을 낼 수 있는가에 대한 논의도 포함되며, 이는 습관 학습(habit learning)이나 multitask learning, 계층적 정책 학습(hierarchical policy learning) 등과 관련된 논의로 이어진다.

감정(emotion)과의 연결 가능성

마지막으로, 감정 상태가 특정 반응을 유도하는 경향성(bias)을 형성하는 데 default policy가 중요한 역할을 할 수 있으며, 이는 감정의 행동 조절 기능에 대한 계산 이론적 설명을 제공할 수 있는 출발점이 될 수 있다고 제안한다.