Mastering Diverse Domains through World Models
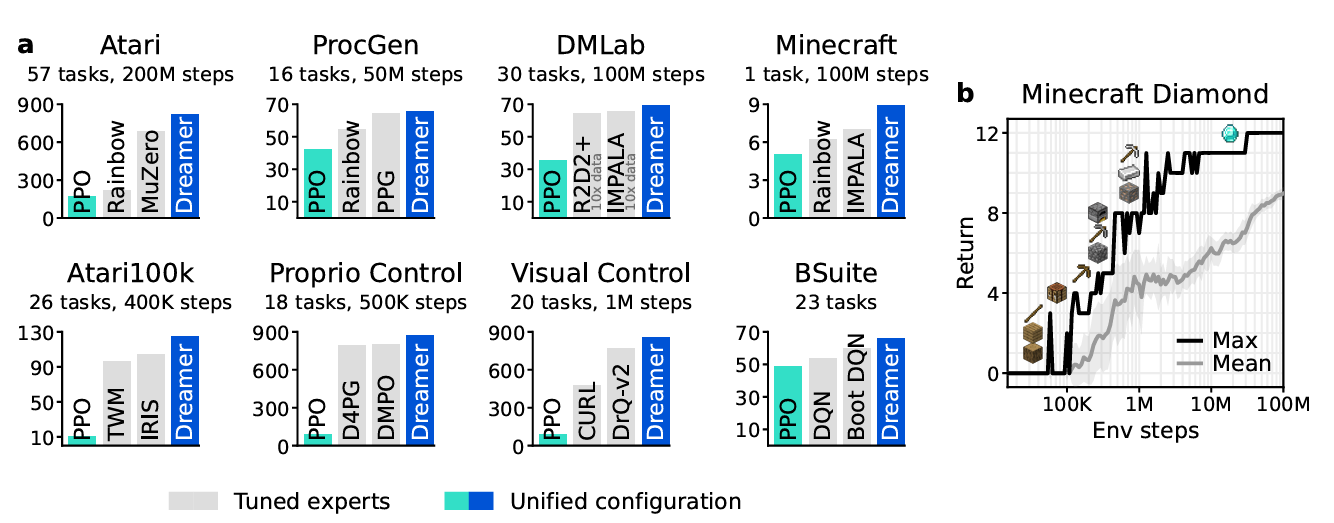
범용적인 강화학습 알고리즘을 개발하는 것은 인공지능 분야의 오랜 도전 과제이다. 기존 강화학습 알고리즘들은 특정 과업에 대해 잘 작동하지만, 새로운 분야에 적용하기 위해서는 많은 인간 전문가의 개입과 실험이 필요하다. DreamerV3는 이러한 한계를 극복하고, 하나의 설정(configuration)으로 150개 이상의 다양한 과업에서 특화된 기존 알고리즘들을 능가하는 성능을 보인다. 이 알고리즘은 환경의 모델을 학습하고, 그 모델을 이용해 미래 상황을 상상(imagination)하면서 행동 정책을 개선한다. 또한 정규화(normalization), 균형 조정(balancing), 변환(transformations) 등의 견고성 기법을 통해 다양한 도메인에서도 안정적인 학습을 가능하게 한다.
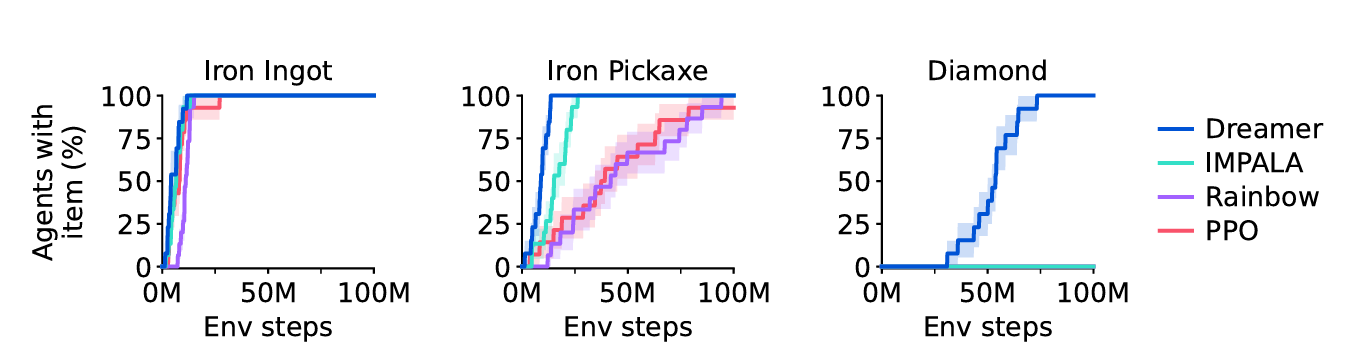
특히 DreamerV3는 기존에 인간 데이터나 도메인 특화된 커리큘럼 없이 해결하기 어려웠던 과제인 Minecraft에서 다이아몬드 채취를 인간의 개입 없이 처음으로 성공한 알고리즘이다. 이 과제는 픽셀 기반의 관찰, 드문 보상(sparse reward), 장기 전략이 필요한 개방형 세계에서의 문제로, 강화학습 연구에서 중요한 도전 과제로 여겨져 왔다. DreamerV3는 이처럼 어려운 제어 문제도 별도의 실험 없이 해결함으로써, 강화학습의 실용적인 적용 범위를 크게 확장시킬 수 있음을 보여준다.
Introduction
현재 강화학습 분야의 표준 알고리즘으로는 PPO(Proximal Policy Optimization)가 널리 사용되지만, 실제로는 특정 도메인에 맞춰 성능을 극대화하기 위해 더 특화된 알고리즘들이 사용된다. 예를 들어, 연속 제어, 이산 행동, 희소 보상, 이미지 기반 입력, 공간 환경, 보드게임 등 각 도메인은 고유한 도전 과제를 가지며, 이에 따라 하이퍼파라미터 튜닝이나 알고리즘 설정이 필수적이다. 이런 설정 과정은 새로운 도메인에 RL을 적용하는 데 큰 장벽이 되며, 특히 계산 자원이 제한되거나 반복 실험이 어려운 경우 강화학습의 활용을 어렵게 만든다.
이러한 배경에서 Dreamer는 “한 번의 설정으로 다양한 도메인을 학습 가능한 일반 알고리즘”이라는 핵심 목표를 가진다. Dreamer의 핵심 아이디어는 ‘world model’을 학습하는 것이다. 이 world model은 에이전트가 환경을 인식하고 미래를 상상할 수 있게 해주는 역할을 하며, world model을 이용한 접근 방식은 이론적으로 매력적이지만, 실제로는 안정적으로 학습하고 강력한 성능을 내는 것이 난제로 여겨져 왔다.

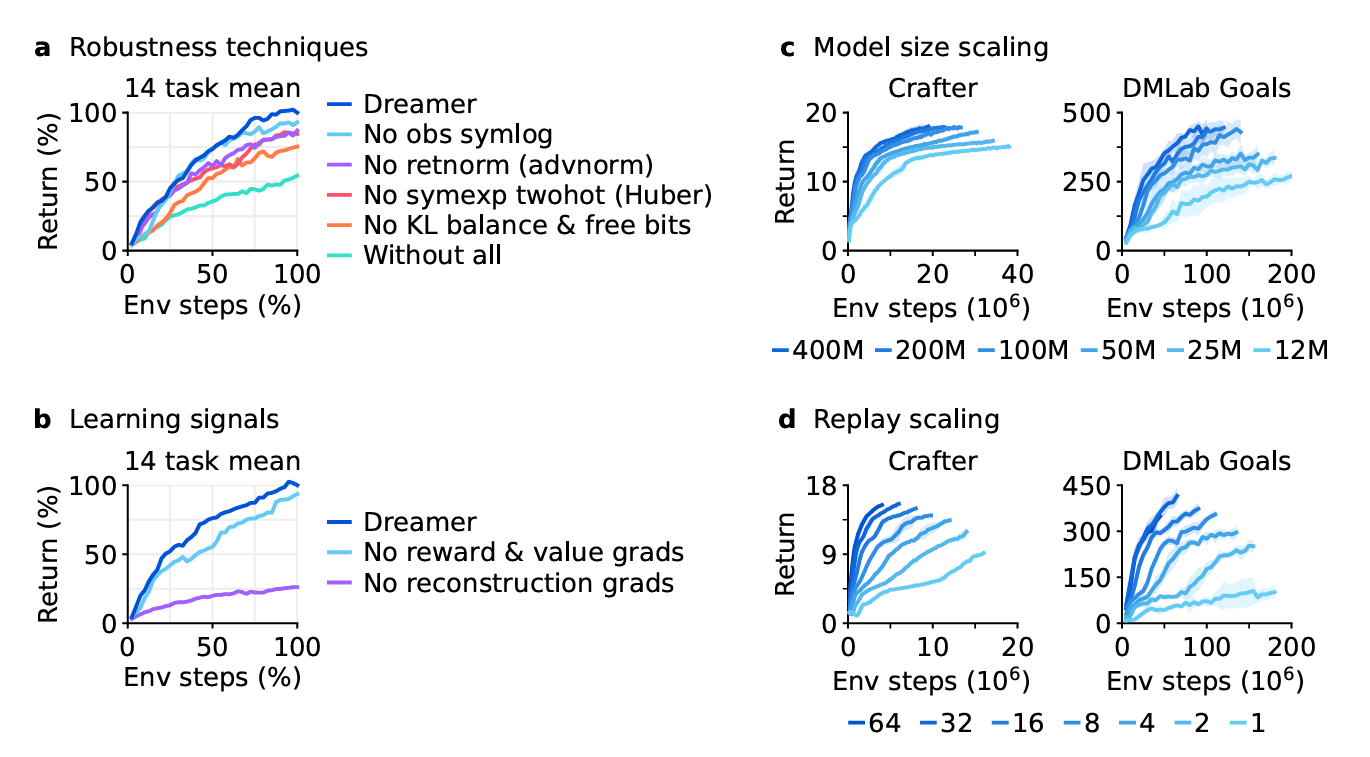
Dreamer는 이를 극복하기 위해 정규화, 균형 조정, 데이터 변환 등 다양한 강인성(robustness) 기법을 도입한다. 이러한 기법은 단순한 이론적 가능성을 넘어서, 실제로 150개 이상의 다양한 과제들에서 일관되게 강력한 성능을 보여주며 모델 크기나 학습 예산이 다르더라도 성능이 안정적으로 향상된다는 패턴을 보여준다. 특히 모델이 클수록 더 적은 상호작용만으로도 더 높은 점수를 얻을 수 있다는 점이 강조된다.
이러한 Dreamer의 가능성을 극단적으로 시험해보기 위해 저자들은 오픈월드 게임인 Minecraft에 Dreamer를 적용하였다. Minecraft는 희소 보상, 긴 시간 지연, 복잡한 탐색, 다양한 환경 변화 등으로 인해 AI 분야에서 ‘다이아몬드 수집’이라는 과제가 대표적인 난제로 간주되어 왔다. 지금까지의 접근 방식은 전문가 데이터나 맞춤형 커리큘럼에 의존해왔으나, Dreamer는 이러한 도움 없이도 ‘처음부터’ 다이아몬드를 수집하는 데 성공한 최초의 알고리즘이다.
Learning algorithm
DreamerV3는 Dreamer 알고리즘의 세 번째 세대로, 세 가지 핵심 신경망 구성 요소로 이루어진다. 이들은 각각 1. 가능한 행동의 결과를 예측하는 world model, 2. 예측된 결과의 가치를 판단하는 critic, 3. 가장 가치 있는 결과를 향해 행동을 선택하는 actor이다. 이 세 구성 요소는 에이전트가 환경과 상호작용하면서 수집한 경험을 replay buffer로부터 샘플링하여 동시에 학습된다.
DreamerV3의 주요 목표는 단일 설정(fixed hyperparameters)으로 다양한 도메인에서 잘 작동하는 범용 알고리즘을 만드는 것이다. 이를 위해서는 각 구성 요소가 입력 신호의 크기나 분포가 다를 수 있는 상황에서도 견고하게 학습되어야 하며, 손실 함수 내의 다양한 항들을 적절히 균형 잡는 것이 중요하다. 이는 같은 도메인 내 유사한 과제가 아니라, 전혀 다른 도메인 간 학습을 목표로 할 때 특히 어려운 과제다.
이 섹션에서는 world model, critic, actor 각각의 구조와 역할뿐 아니라, 이들이 사용하는 robust loss functions에 대해 소개하고, 스케일이 명확하지 않은 수치들을 안정적으로 예측하기 위한 다양한 정규화 및 균형 조정 기법들도 함께 제안한다. DreamerV3의 학습 알고리즘은 단순한 구조적 설계를 넘어서, 다양한 환경 조건에서도 안정적으로 학습할 수 있는 견고성(robustness)을 핵심으로 하고 있다.
World model learning
DreamerV3의 world model은 센서 입력을 autoencoding 방식으로 압축하여 표현하고, 이후 가능한 행동들의 결과를 예측함으로써 planning을 가능하게 한다. 이를 위해 사용된 모델은 Recurrent State-Space Model (RSSM)이며, Figure 3에 그 구조가 시각화되어 있다.
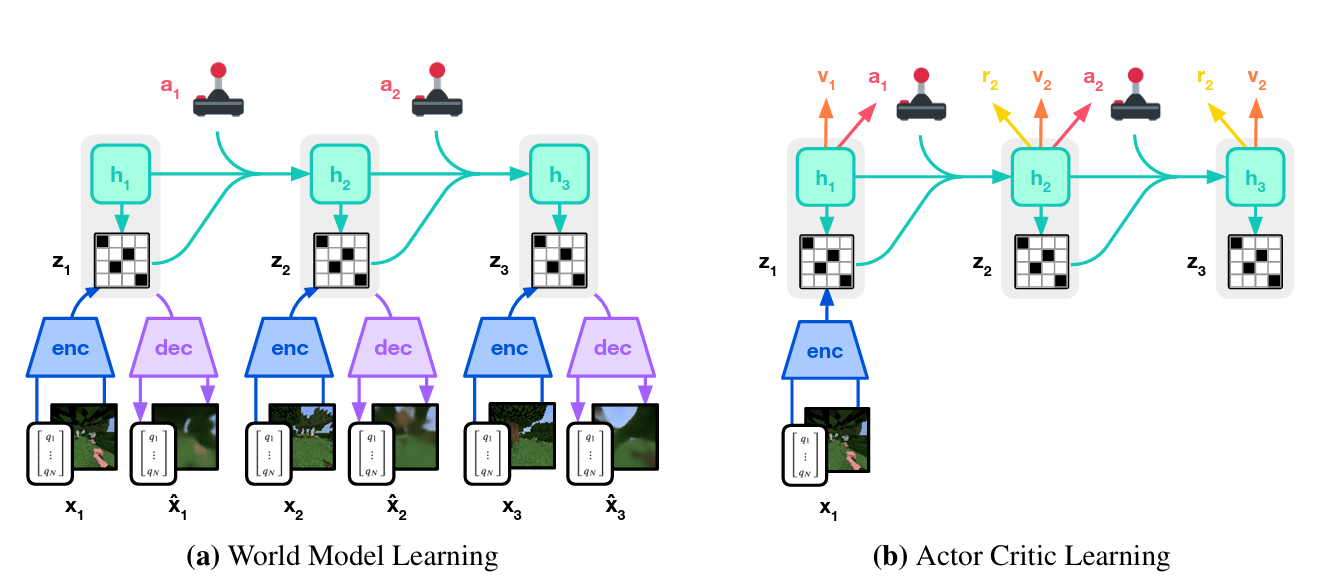
RSSM에서는 먼저 encoder가 현재 센서 입력 \(x_t\)를 확률적 표현 \(z_t\)로 변환한다. 이어서 recurrent state \(h_t\)를 유지하는 sequence model이 이전 상태 \(h_{t-1}\), \(z_{t-1}\), 행동 \(a_{t-1}\)를 기반으로 다음 상태를 예측한다. 이때 \(h_t\)와 \(z_t\)의 결합이 현재의 모델 상태가 되며, 이 상태로부터 reward \(r_t\), episode의 계속 여부 \(c_t ∈ {0, 1}\), 그리고 입력 \(x_t\)를 재구성하게 된다.
모델 구조는 다음 수식으로 요약된다:
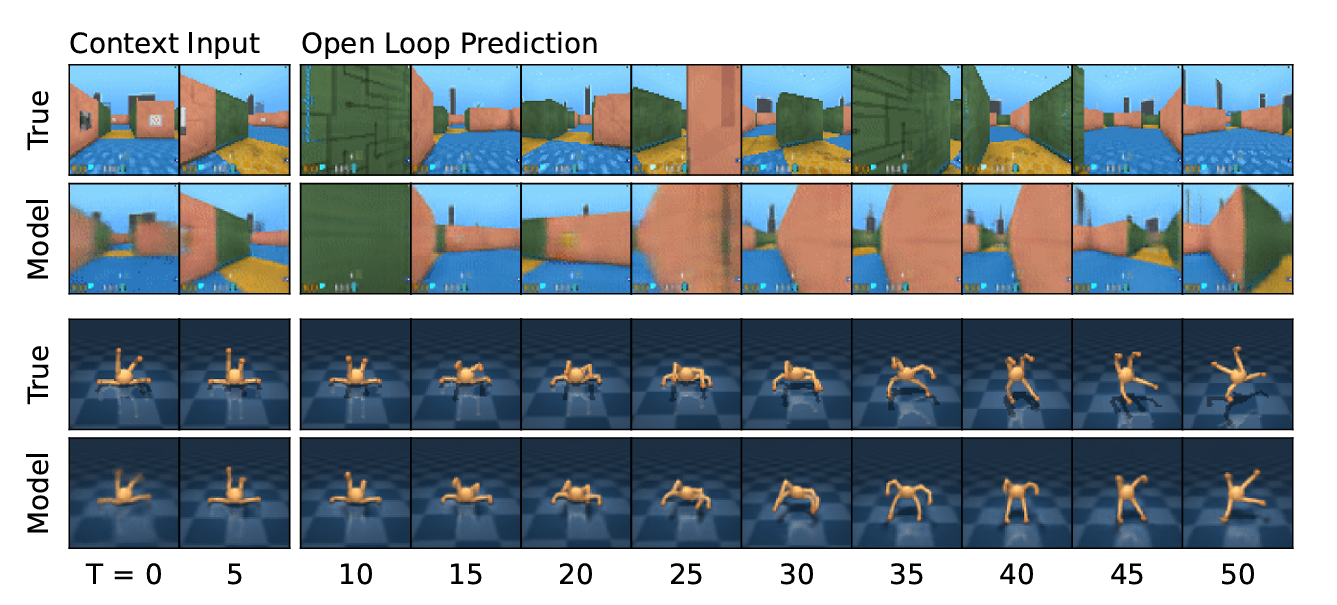
\[\text{Sequence model: } h_t = f_\phi(h_{t-1}, z_{t-1}, a_{t-1}) \\ \text{Encoder: } z_t \sim q_\phi(z_t | h_t, x_t) \\ \text{Dynamics predictor: } \hat{z}_t \sim p_\phi(\hat{z}_t | h_t) \\ \text{Reward predictor: } \hat{r}_t \sim p_\phi(\hat{r}_t | h_t, z_t) \\ \text{Continue predictor: } \hat{c}_t \sim p_\phi(\hat{c}_t | h_t, z_t) \\ \text{Decoder: } \hat{x}_t \sim p_\phi(\hat{x}_t | h_t, z_t)\]Figure 4는 이 모델이 수행하는 장기 비디오 예측의 시각화를 보여준다. encoder와 decoder는 CNN을 통해 이미지 입력을 처리하고, MLP를 사용해 벡터 입력을 처리한다. reward, continue predictor, dynamics predictor는 모두 MLP로 구현되어 있다. 표현 \(z_t\)는 softmax 분포에서 샘플링되며, gradient는 straight-through 방식으로 전달된다.
학습은 입력 \(x_{1:T}\), 행동 \(a_{1:T}\), 보상 \(r_{1:T}\), 플래그 \(c_{1:T}\)로 구성된 시퀀스를 받아 이루어지며, 손실 함수는 다음과 같다:
\[L(\phi) = \mathbb{E}_{q_\phi} \left[ \sum_{t=1}^T (\beta_{\text{pred}} L_{\text{pred}}(\phi) + \beta_{\text{dyn}} L_{\text{dyn}}(\phi) + \beta_{\text{rep}} L_{\text{rep}}(\phi)) \right]\]여기서 각 항의 weight는 \(β_{pred}\) = 1, \(β_{dyn}\) = 1, \(β_{rep}\) = 0.1이다. 예측 손실 \(L_{pred}\)는 symlog 제곱 손실을 사용하여 decoder, reward, continue predictor를 학습한다. dynamics 손실 \(L_{dyn}\)는 KL divergence를 통해 다음 표현을 예측하는 sequence model을 학습한다:
\[L_{\text{dyn}}(\phi) = \max(1, \text{KL}[ \text{sg}(q_\phi(z_t | h_t, x_t)) || p_\phi(z_t | h_t) ])\]표현 손실 L_{rep}는 표현을 더 예측 가능하게 만들도록 학습한다:
\[L_{\text{rep}}(\phi) = \max(1, \text{KL}[ q_\phi(z_t | h_t, x_t) || \text{sg}(p_\phi(z_t | h_t)) ])\]degenerate solution을 피하기 위해, free bits 기법을 사용하여 KL 손실을 1 nat (≈ 1.44 bits) 이하로는 반영하지 않는다. 이는 dynamics나 representation 손실이 이미 잘 수렴된 경우 학습의 중점을 prediction loss로 전환하기 위함이다.
또한, 다양한 환경의 시각적 복잡도에 대응하기 위해 이전에는 \(β_{rep}\)를 조절해야 했지만, 여기서는 free bits와 소규모 representation loss를 결합하여 고정된 하이퍼파라미터로도 안정적인 학습이 가능하게 하였다. 추가적으로 symlog 변환을 통해 벡터 입력의 큰 값과 그로 인한 reconstruction gradient 폭주를 방지하였다.
마지막으로 KL 손실의 스파이크를 방지하기 위해 encoder와 dynamics predictor의 categorical distribution은 1%의 균일 분포와 99%의 neural net 출력을 섞은 방식으로 파라미터화된다. 이로 인해 모델은 결정론적으로 변할 수 없으며 KL 손실이 안정적으로 유지된다.
Critic learning
DreamerV3에서의 critic 학습은 world model이 생성한 상상 trajectory를 기반으로 수행된다. actor와 critic은 recurrent world model이 제공하는 Markov 표현인
\[s_t = \{h_t, z_t\}\]를 입력으로 받아 동작하며, actor는 상태별 누적 보상인 return
\[R_t = \sum_{\tau=0}^{\infty} \gamma^\tau r_{t+\tau}\]을 최대화하는 행동을 선택한다. 여기서 할인율은 \(\gamma = 0.997\)로 고정된다. critic은 현재 정책에 따른 상태별 return 분포를 예측하는데, 이를 위해 bootstrapped λ-return을 사용하며, 아래와 같이 정의된다:
\[R_t^\lambda = r_t + \gamma c_t \left[(1 - \lambda) v_t + \lambda R_{t+1}^\lambda\right], \quad R_T^\lambda = v_T\]critic은 이 값을 최대우도법에 기반해 학습하며 손실 함수는 다음과 같다:
\[\mathcal{L}(\psi) = -\sum_{t=1}^T \log p_\psi(R_t^\lambda \mid s_t)\]예측값 \(v_t = \mathbb{E}[v_\psi(\cdot \mid s_t)]\)은 분포의 기대값으로 정의된다. 다양한 환경에서 return의 분포는 다봉(multi-modal)이거나 값의 범위가 커질 수 있기 때문에, DreamerV3는 critic의 출력 분포를 정규분포 대신 지수 간격의 categorical distribution으로 파라미터화한다. 이 방식은 gradient의 크기를 target의 크기와 분리하여 안정성을 높인다.
보상 예측이 어려운 환경에서도 value prediction을 향상시키기 위해 critic loss는 두 종류의 trajectory에 대해 계산된다. 상상 trajectory에는 손실 가중치를 \(\beta_{\text{val}} = 1\)로, replay buffer에서 샘플링한 trajectory에는 \(\beta_{\text{repval}} = 0.3\)을 적용한다. replay trajectory의 λ-return 계산 시, imagination rollout의 시작 지점에서 계산된 \(R_t^\lambda\) 를 on-policy value로 사용한다.
critic이 자신의 예측값을 다시 학습 target으로 삼기 때문에, 학습 안정성을 위해 critic의 출력이 자신의 EMA(exponential moving average)에 수렴하도록 regularization을 적용한다. 이는 기존 target network 기법과 유사하지만, DreamerV3는 현재 critic 네트워크를 그대로 사용하면서도 안정적인 return 계산이 가능하다는 특징이 있다.
또한, 학습 초기 reward predictor와 critic이 무작위로 초기화되었을 때 과도한 보상을 예측하는 문제가 발생할 수 있다. 이를 방지하기 위해 두 네트워크의 출력 weight matrix를 0으로 초기화하여 초반 학습을 안정화하고 빠르게 진행되도록 한다.
Actor learning
DreamerV3에서 actor는 주어진 상태에서 return을 최대화하도록 행동을 학습하며, 이 과정에서 entropy regularizer를 사용해 탐색을 유도한다. 그러나 환경마다 보상의 스케일과 빈도가 다르기 때문에, 고정된 entropy scale을 사용하려면 보상의 크기에 따라 탐색량이 지나치게 민감해지는 문제를 해결해야 한다. 이를 위해 return 값을 정규화(normalization)하여 약 \([0, 1]\)구간에 포함되도록 조정한다. 구체적으로, actor의 손실 함수는 다음과 같은 surrogate objective로 정의된다:
\[\mathcal{L}(\theta) = - \sum_{t=1}^{T} \text{sg}\left(\frac{R_t^\lambda - v_\psi(s_t)}{\max(1, S)}\right) \log \pi_\theta(a_t \mid s_t) + \eta \, \mathcal{H}[\pi_\theta(a_t \mid s_t)]\]여기서 \(\eta = 3 \times 10^{-4}\)는 고정된 entropy 스케일이며, \(\text{sg}(\cdot)\)는 stop-gradient 연산, \(R_t^\lambda\)는 λ-return, \(v_\psi(s_t)\)는 critic의 예측값이다. 정규화 분모인 \(S\)는 전체 return 배치에서 95번째 백분위수와 5번째 백분위수의 차이로 정의되며, 지수 이동 평균으로 부드럽게 갱신된다:
\[S = \text{EMA}\left(\text{Per}(R_t^\lambda, 95) - \text{Per}(R_t^\lambda, 5), 0.99\right)\]이처럼 백분위수를 사용한 이유는 극단적인 이상값(outlier)에 대한 민감도를 줄이기 위함이다. 반면, 단순히 최소값과 최대값을 사용하면 이상치 때문에 전체 return이 과도하게 축소되어 성능 저하가 발생할 수 있다.
기존 연구들은 일반적으로 return이 아니라 advantage를 정규화했으며, \(A_t = R_t^\lambda - v_\psi(s_t)\) 이 경우, 보상이 드문 환경에서는 작은 advantage의 variance를 키우는 과정에서 entropy 항보다 노이즈가 커져 탐색이 정체될 수 있다. 또한, reward를 표준편차로 정규화하는 방식은 sparse reward 환경에서 분모가 거의 0에 가까워질 수 있어 보상의 왜곡이 심해진다.
또한, constrained optimization 접근법은 상태 평균의 entropy를 일정 수준으로 유지하도록 하지만, sparse reward 환경에서는 탐색 속도가 느리고 dense reward 환경에서는 수렴 성능이 낮아지는 문제가 있다. 이에 비해 DreamerV3의 return normalization은 이러한 기존 방식들의 한계를 극복하고, 다양한 도메인에서 안정적인 탐색과 높은 성능 수렴을 동시에 달성한다.
Robust predictions
Results
Previous work
Conclusion