Successor Features for Transfer in Reinforcement Learning

이전의 ‘The hippocampus as a predictive map’ 논문에서도 SR에 관련된 내용을 다루었고, 이 논문에서도 그럴 것이다. 하지만 두 논문이 Successor feature/representation을 다루는 방식에는 약간의 차이가 있기에, 이 부분을 먼저 짚고 넘어가려고 한다. Stachenfeld et al. (2017, 이전 논문)에서 상태 가치 함수 (State Value Function)는 다음과 같이 표현될 수 있다.

\[V(s) = \mathbb{E}_\pi \left[ \sum_{t=0}^{\infty} \gamma^t R(s_t) \mid s_0 = s \right]\]

그리고 Barreto et al. (2017, 본 논문)에서의 행동-가치 함수 Q는 다음과 같이 표현할 수 있다.

\[Q^\pi(s, a) = \mathbb{E}_\pi \left[ \sum_{t=0}^{\infty} \gamma^t r(s_t, a_t, s_{t+1}) \mid s_0 = s, a_0 = a \right]\]

또한 Barreto et al.에서 r은 다음과 같이 표현할 수 있다고 가정하겠다.

\[r(s, a, s') = \phi(s, a, s')^\top w\]

그리고 Stachenfeld의 논문에서 정의한 Successor Representation의 정의, 그리고 상태 가치 함수 V는 다음과 같이 표현될 수 있다.

\[M = \sum_{t=0}^{\infty} \gamma^t T^t = (I - \gamma T)^{-1}\] \[V = M R\]

또한 Barreto의 논문에서의 Successor Feature의 정의는 다음과 같이 표현할 수 있다.

\[\psi^\pi(s,a) = \mathbb{E}_\pi \left[ \sum_{t=0}^{\infty} \gamma^t \phi(s_t, a_t, s_{t+1}) \mid s_0 = s, a_0 = a \right]\] \[\begin{aligned} Q^\pi(s, a) &= \mathbb{E}_\pi \left[ r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \cdots \mid S_t = s, A_t = a \right] \\ &= \mathbb{E}_\pi \left[ \phi_{t+1}^\top w + \gamma \phi_{t+2}^\top w + \gamma^2 \phi_{t+3}^\top w + \cdots \mid S_t = s, A_t = a \right] \\ &= \left( \mathbb{E}_\pi \left[ \sum_{i=t}^{\infty} \gamma^{i - t} \phi_{i+1} \mid S_t = s, A_t = a \right] \right)^\top w \\ &= \psi^\pi(s, a)^\top w \end{aligned}\]

ϕ(s, a, s’)는 feature vector로 보통은 어떤 임의의 함수 ϕ = S × A × S → ℝⁿ 형태다. 그런데 지금 상황에서는 ϕ가 one-hot 벡터라고 가정해 보자. 이 말은 특정 (s’, a’)가 주어졌을 때 ϕ(s, a, s’)는 벡터의 특정 위치에서만 1이고 나머지는 0이라는 뜻이다. 즉, 각 (s, a, s′) 쌍마다 feature vector ϕ(s, a, s′)는 다음과 같은 벡터다:

\[\phi(s, a, s') = e_{(s', a')} \quad \text{(some fixed index depending on } s', a')\]

여기서 \(e_{(s', a')}\)는 feature vector의 특정 위치가 1이고 나머지는 0인 standard basis vector다. 이 의미는 곧, ϕ가 어떤 미래 state-action pair (s′, a′)가 발생했는지를 인디케이터 벡터로 나타낸다는 뜻이다. Barreto et al.의 SF 정의를 다시 보자:

\[\psi^\pi(s, a) = \mathbb{E}_\pi \left[ \sum_{t=0}^{\infty} \gamma^t \phi(s_t, a_t, s_{t+1}) \mid s_0 = s, a_0 = a \right]\]

이 정의는, 시작점 (s, a)에서 출발해 policy π를 따라 행동할 때, 미래에 발생하는 (s′, a′) pair들의 ϕ값을 누적한 것이다. 그런데 만약 ϕ가 one-hot이라면? 각 시점 t에서 ϕ(s_t, a_t, s_{t+1})는 다음과 같다:

\[\phi(s_t, a_t, s_{t+1}) = e_{(s_{t+1}, a_{t+1})}\]

여기서 a_{t+1}는 policy π에 따라 확률적으로 정해지므로, expectation 안에서는 e_{(s’, a’)}의 기대값으로 남는다. 중요한 것은, 이 기대값은 결국, 현재 (s, a)에서 시작했을 때, (s’, a’)가 미래에 몇 번 등장하는지의 할인된 기대값이다. 따라서, ψ^π(s, a)의 각 원소는 다음을 나타낸다:

\[\psi^\pi(s, a)[(s', a')] = \mathbb{E}^\pi \left[ \sum_{t=0}^{\infty} \gamma^t \mathbb{I}[s_t = s', a_t = a'] \mid s_0 = s, a_0 = a \right]\]

이는 정확히 (s, a)에서 시작했을 때 미래에 (s′, a′)를 방문할 할인된 기대 횟수를 뜻한다. 이 정의는 우리가 SR에서 사용한 정의와 구조적으로 동일하다. 그리고 Stachenfeld et al.에서의 Successor Representation은 다음과 같다:

\[M(s, s') = \mathbb{E}_\pi \left[ \sum_{t=0}^{\infty} \gamma^t \mathbb{I}[s_t = s'] \mid s_0 = s \right]\]

이 정의는 미래에 상태 s′에 몇 번 방문하는지를 나타낸다. 여기서는 action은 명시적으로 고려되지 않지만, 만약 (s, a)-pair를 상태로 간주하면 구조는 완전히 같다. 이러한 논리는 Barreto et al. 논문에서도 명시적으로 언급되며, SR이 SF의 특수한 경우임을 보여준다. SF는 SR의 구조를 일반화해 feature space로 확장하며, 이로써 transfer learning에 더 적합한 구조를 갖추게 된다.

1. Introduction

이 논문은 강화학습(Reinforcement Learning, RL)의 전이 학습(transfer learning)에 초점을 맞추며, 특히 동일한 환경 내에서 보상 함수만 달라지는 다양한 하위 과제(subtask) 간의 전이를 다룬다. 논문에서 제안하는 방법은 다음 두 가지 개념적 기반 위에 세워져 있다:

Successor feature는 기존 Dayan의 Successor Representation(SR)을 일반화한 개념으로, 상태를 미래의 상태 방문 확률이 아닌 feature space에서의 예측으로 표현한다. 이는 연속적인 상태 공간(continuous state space)에도 적용 가능하며, 환경의 dynamics와 보상을 분리해서 표현할 수 있다는 점에서 전이 학습에 유리하다. 즉, 환경이 동일하고 보상 구조만 달라질 때, dynamics에 해당하는 SF만 재활용하면 새로운 가치 함수(Q)를 빠르게 계산할 수 있다. 또한 기존 Bellman 이론은 단일 정책에 대해 정의되었으나, 이 논문에서는 다수의 기존 정책들로부터 새로운 과제에서의 성능 보장을 제공하는 일반화된 이론을 제시한다. 이를 통해 새로운 과제에 대해 학습을 수행하기 전부터 어느 정도 성능을 예측할 수 있으며, 이를 기반으로 재사용 가능한 스킬 라이브러리(skill library)를 구축할 수 있다.

논문이 다루는 동일한 환경(즉, 동일한 transition dynamics)을 공유하면서 보상 구조만 다른 과제들 간의 전이 시나리오는 다음과 같다. 에를 들어서 운전 과제를 운전대 조작 → 우회전 → 목적지 도달의 계층적 하위 과제로 나눌 수 있다면, 이들 간의 지식 공유가 가능해야 한다고 말하고 있다. 이러한 전이 과정은 별도의 모듈이 아닌 강화학습 내부 구조에 자연스럽게 통합되어야 하며, 과제 간 정보를 유연하게 공유할 수 있어야 한다고 주장한다.

2. Background and problem formulation

MDP는 다음과 같은 5-튜플로 정의된다:

• $\mathcal{S}$: 상태(state)의 집합
• $\mathcal{A}$: 행동(action)의 집합
• $p(\cdot \mid s, a)$: 상태 $s$에서 행동 $a$를 취했을 때 다음 상태로의 확률 분포 (transition dynamics)
• $R(s, a, s’)$: 전이 $s \xrightarrow{a} s’$ 에서 얻는 보상 (보통 기대값 $r(s,a,s’)$를 사용)
• $\gamma \in [0,1)$: 미래 보상에 대한 할인 계수 (discount factor)

또한 에이전트의 목표는 정책(policy) $\pi$를 찾아서 기대 누적 보상 (return)

\[G_t = \sum_{i=0}^{\infty} \gamma^i R_{t+i+1}\]

을 최대화하는 것이다. 이때 사용하는 핵심 개념은 가치 함수(value function)이며, 특히 행동-가치 함수(action-value function)는 다음과 같이 정의된다:

\[Q^\pi(s,a) = \mathbb{E}_\pi \left[ G_t \mid S_t = s, A_t = a \right]\]

$\pi$에 대한 $Q^\pi$가 주어지면, 이를 이용해 탐욕적(greedy) 정책 $\pi’$를 만들 수 있다:

\[\pi'(s) \in \arg\max_a Q^\pi(s, a)\]

이때 $\pi’$는 $\pi$보다 성능이 같거나 더 나은 정책임이 보장된다. 이와 같이 정책 평가(policy evaluation)와 정책 개선(policy improvement)을 반복함으로써 최적 정책 $\pi^*$에 수렴할 수 있다. 또한 이 논문에서 전이 transition은 다음과 같이 정의된다:

작업 집합(task set) $\mathcal{T}$와 그 부분집합 $\mathcal{T}’ \subset \mathcal{T}$가 있을 때, $\mathcal{T}$에서 학습한 후 어떤 과제 $t \in \mathcal{T}$에 대해 $\mathcal{T}’$에서만 학습했을 때보다 항상 더 나은(혹은 같은) 성능을 보인다면, 전이가 이루어진 것이다. 논문에서는 하나의 과제(task)를 동일한 MDP 하에서의 보상 함수 $R(s,a,s’)$의 구체적인 정의로 본다.

3. Successor features

Barreto는 보상 함수가 다음과 같이 표현될 수 있다고 가정한다:

\[r(s, a, s') = \phi(s, a, s')^\top w\]

여기서 $\phi(s, a, s’)$는 $(s, a, s’)$ transition의 feature vector이며, $w$는 각 feature에 대응하는 가중치 벡터이다. 이 표현은 일반성을 잃지 않으며, $\phi_i(s, a, s’) = r(s, a, s’)$인 단일 feature로도 임의의 보상 함수를 구성할 수 있다.

정의된 $r(s, a, s’)$를 이용해 Q-함수를 다음과 같이 전개할 수 있다:

\[Q^\pi(s, a) = \mathbb{E}_\pi \left[ r_{t+1} + \gamma r_{t+2} + \cdots \mid S_t = s, A_t = a \right]\]

보상을 $\phi^\top w$로 표현하면,

\[\begin{aligned} Q^\pi(s, a) &= \mathbb{E}_\pi \left[ \phi_{t+1}^\top w + \gamma \phi_{t+2}^\top w + \cdots \mid S_t = s, A_t = a \right] \\ &= \mathbb{E}_\pi \left[ \sum_{i=t}^\infty \gamma^{i-t} \phi_{i+1} \mid S_t = s, A_t = a \right]^\top w \\ &= \psi^\pi(s, a)^\top w \end{aligned}\]

여기서 $\psi^\pi(s, a)$는 Successor Feature (SF)이며, 정책 $\pi$ 하에서 상태-행동 쌍 $(s, a)$로부터 시작해 미래에 얼마나 많이 각 피처가 발생할지를 할인된 기대값으로 나타낸다. 그리고 Successor Feature는 아래와 같은 Bellman equation을 만족한다:

\[\psi^\pi(s, a) = \phi(s, a, s') + \gamma \mathbb{E}_\pi \left[ \psi^\pi(s', \pi(s')) \right]\]

이 식은 SR이 미래 상태 방문 횟수를 기대값으로 나타내듯이, SF는 미래 피처 발생을 기대값으로 나타낸다는 점에서 동일한 구조를 가진다. 특히 $\phi(s, a, s’)$가 $(s’, a’)$에 대해 one-hot 인코딩이라면, 이 피처는 단순히 미래 특정 전이의 존재를 인디케이터로 나타낸다. 이때 SF는 다음과 같이 해석할 수 있다:

\[\psi^\pi(s,a) = \mathbb{E}_\pi \left[ \sum_{t=0}^\infty \gamma^t \mathbb{I}[(s_t, a_t, s_{t+1}) = (s', a', s'')] \mid s_0 = s, a_0 = a \right]\]

이는 바로 SR의 일반화로 볼 수 있으며, SR은 SF의 특수한 형태로 해석된다. 이런 방식으로 SF는 기존 SR 구조를 피처 공간으로 확장한 것으로, 보상 함수의 변경에도 빠르게 적응할 수 있는 유연한 표현을 제공한다.

4. Transfer via successor features

먼저, 논문은 다음과 같은 가정 하에서 전이를 정의한다: 환경의 상태 공간 $\mathcal{S}$, 행동 공간 $\mathcal{A}$, 전이 함수 $p$, 할인 인자 $\gamma$는 고정되어 있고, 오직 보상 함수만이 달라진다. 보상 함수는 다음과 같이 피처 표현 $\phi(s, a, s’)$와 가중치 벡터 $w$의 내적 형태로 표현된다:

\[r(s,a,s') = \phi(s,a,s')^\top w\]

따라서 $\phi$가 고정되어 있다면, $w$를 바꾸는 것으로 서로 다른 MDP(과제, task)를 정의할 수 있다. 이렇게 정의된 모든 MDP들의 집합을 다음과 같이 표현한다:

\[\mathcal{M}_\phi(\mathcal{S}, \mathcal{A}, p, \gamma) \equiv \left\{ M(\mathcal{S}, \mathcal{A}, p, r, \gamma) \mid r(s,a,s') = \phi(s,a,s')^\top w \right\}\]

이처럼 보상 가중치 $w$에 따라 달라지는 MDP를 “task”라고 간주하며, 이 집합 내에서의 전이 문제를 해결하는 것이 논문의 목표다.

실제 예시로는, 동물이 “배고픈 상태”에서는 음식에 보상을 주고, “목마른 상태”에서는 물에 보상을 주는 상황이 있다. 여기서 $w$는 해당 순간의 “선호(taste)”를 나타내는 벡터로 해석될 수 있다. 다른 예시로는, 상품의 생산 프로세스는 동일하지만, 시장 가격(w)이 변화하는 경우가 있다. 이런 경우 과거 경험으로부터 학습한 정책을 바탕으로 새로운 환경에서도 빠르게 적응할 수 있어야 한다.

본 논문에서는 이전 task 집합 $\mathcal{M} = {M_1, M_2, \dots, M_n}$에서 학습한 경험을 바탕으로, 새로운 과제 $M_{n+1}$에서 어떤 초기 정책 $\pi$를 생성할 수 있어야 하며, 이 정책은 이전 task의 일부 $M’ \subset \mathcal{M}$에서만 학습했을 때 얻는 정책 $\pi’$보다 항상 같거나 더 높은 성능($Q^\pi(s, a) \geq Q^{\pi’}(s, a)$)을 보장해야 한다.

이를 해결하기 위해, 저자들은 먼저 기존 dynamic programming(DP)의 policy improvement 개념을 일반화하고, 이 일반화된 형태를 SF를 통해 효율적으로 구현할 수 있음을 보인다.

4.1. Generalized policy improvement

우선, 강화학습에서 중심이 되는 이론 중 하나는 Bellman의 정책 개선 정리(Policy Improvement Theorem) 이다. 이 정리는 어떤 정책 $\pi$의 가치 함수 $Q^\pi$에 대해 greedy하게 행동을 선택하면 기존 정책보다 성능이 떨어지지 않는 새로운 정책을 얻을 수 있다는 것을 보장한다. 이러한 정리는 동적 프로그래밍(DP)의 근간이자 많은 RL 알고리즘이 따르는 원칙이다.

저자는 이러한 정리를 여러 개의 정책 $\pi_1, \pi_2, …, \pi_n$이 존재할 때로 확장한다. 이 확장은 다음과 같은 상황을 다룬다: 여러 개의 정책들이 있고, 각각의 정책에 대한 Q-value 함수(혹은 그 근사값)가 존재한다고 하자. 이때 우리는 각 정책의 가치 함수 중에서 가장 높은 값을 가지는 행동을 선택해 새로운 정책 $\pi$를 구성할 수 있으며, 이 새로운 정책은 모든 기존 정책보다 나쁘지 않다는 보장을 갖는다. 이를 Generalized Policy Improvement (GPI) 라고 부른다.

각 정책 $\pi_i$의 action-value 함수 $Q^{\pi_i}(s,a)$는 근사값 $\tilde{Q}^{\pi_i}(s,a)$로 표현되며, 이때 오차는 최대 $\epsilon$으로 제한된다:

\[\vert Q^{\pi_i}(s,a) - \tilde{Q}^{\pi_i}(s,a) \vert \leq \epsilon, \quad \forall s,a,i\]

그리고 새로운 정책 $\pi$는 다음과 같이 정의된다:

\[\pi(s) \in \arg\max_a \max_i \tilde{Q}^{\pi_i}(s,a)\]

이때 새로운 정책 $\pi$의 진짜 Q-값은 다음의 하한을 만족한다:

\[Q^{\pi}(s,a) \geq \max_i Q^{\pi_i}(s,a) - \frac{2\epsilon}{1 - \gamma}\]

이 정리는 여러 정책 중 어느 하나의 Q-값도 완전히 신뢰하지 않지만, 모든 정책의 Q-값이 일정 수준 이하의 오차만을 포함한다면, 가장 높은 Q값을 기준으로 행동을 결정하는 새로운 정책도 충분히 좋은 성능을 낼 수 있다는 점을 보장한다.

이 결과는 특히 두 가지 상황에서 유용하게 적용될 수 있다. 첫째, 여러 정책이 병렬적으로 평가되는 상황에서, GPI는 이들을 조합하여 좋은 행동을 선택할 수 있는 체계적인 방법을 제공한다. 둘째, 환경이 바뀌는 경우(예: 보상 함수가 바뀌는 transfer learning 설정)에도 이전에 학습한 여러 정책의 Q-값들을 활용해 빠르게 좋은 초기 정책을 생성할 수 있다.

또한, 만약 오차가 없고 ($\epsilon = 0$), 기존의 어떤 정책이 모든 상태에서 항상 다른 정책보다 높은 Q-값을 가진다면, GPI는 기존의 정책 개선 정리와 동일하게 작동하며 더 이상 이전 정책들을 보존할 필요가 없어진다. 하지만, 여러 정책이 서로 다른 상태에서 강점을 가질 경우, GPI는 이들을 상호 보완적으로 활용해 더 강력한 정책을 만들어낸다.

4.2. Generalized policy improvement with successor features

이 부분에서는 Successor Features(SFs) 를 활용한 Generalized Policy Improvement(GPI) 기법을 통해, 어떻게 효율적인 transfer learning이 가능한지를 설명한다. 핵심 아이디어는 여러 과제(task)에 대한 최적 정책을 학습한 이후, 새로운 과제에 대한 정책을 이들로부터 유도할 수 있다는 것이다.

우선, 각 과제 $M_i \in \mathcal{M}\phi$는 고유한 weight vector $w_i \in \mathbb{R}^d$에 의해 정의된다. 이때, 과제 $M_i$의 최적 정책을 \(\pi_i^*\)라고 하고, 그에 따른 action-value function을 \(Q_i^{\pi^*}(s,a)\)라고 하자. 새로운 과제 $M{n+1}$이 등장했을 때, 기존에 학습된 \(\pi_i^*\)들을 $M_{n+1}$에 대해 재사용하는 방식으로 정책을 구성할 수 있다. 단, reward가 $w_{n+1}$로 바뀌었다면, 기존 정책 \(\pi_i^*\)의 성능을 다시 계산해야 한다.

이때 SF가 유용하게 작동한다. 이미 학습된 $\psi^{\pi_i^*}(s,a)$가 존재하고, 새로운 reward vector $w_{n+1}$만 주어지면, 다음과 같이 즉시 Q-function을 계산할 수 있다:

\[Q_{n+1}^{\pi_i^*}(s,a) = \psi^{\pi_i^*}(s,a)^\top w_{n+1}\]

이렇게 계산된 여러 정책들의 Q-function 중 가장 높은 값을 기준으로 행동을 선택하면, GPI를 통해 기존 정책 중 어떤 것보다도 성능이 떨어지지 않는 새로운 정책 $\pi$를 생성할 수 있다. 이 방식은 새로운 task에 대해 RL을 처음부터 다시 수행하는 것보다 훨씬 효율적이다.

이 접근법의 성능은 Theorem 2를 통해 수학적으로 보장된다. 이 정리는 주어진 task $M_i$에 대해, 다른 과제들 $M_j$에서 유도된 최적 정책 \(\pi_j^*\)를 실행했을 때의 성능 \(Q_i^{\pi_j^*}\)와 SF 기반 근사값 \(\tilde{Q}_i^{\pi_j^*}\) 간 오차 $\epsilon$이 작을 경우, $\pi$가 $M_i$에서 최적 정책 대비 얼마나 성능이 떨어질지를 다음과 같이 상한할 수 있다고 보장한다:

\[Q_i^{\pi_i^*}(s,a) - Q_i^{\pi}(s,a) \leq \frac{2}{1 - \gamma} \left( \phi_{\text{max}} \min_j \| w_i - w_j \| + \epsilon \right)\]

이 식에서 중요한 요소는 \(\min_j \vert w_i - w_j \vert\)이다. 즉, 현재 과제 $w_i$와 가장 가까운 과제 $w_j$ 간의 거리(distance)가 작을수록 성능 손실이 적다는 것이다. 이는 곧 유사한 과제를 과거에 본 경험이 있다면, 새로운 과제도 잘 해결할 수 있다는 직관을 수학적으로 뒷받침해 준다.

실제 구현에서 SF를 메모리에 저장해야 하므로, 어떤 SF를 유지할지 결정하는 기준도 이론적으로 도출된다. 예를 들어, 새 과제의 $w_i$가 기존의 어떤 $w_j$와 충분히 멀다면 새로운 SF를 생성하고, 아니라면 기존 것을 재활용하거나 교체할 수 있다.

5. Experiments

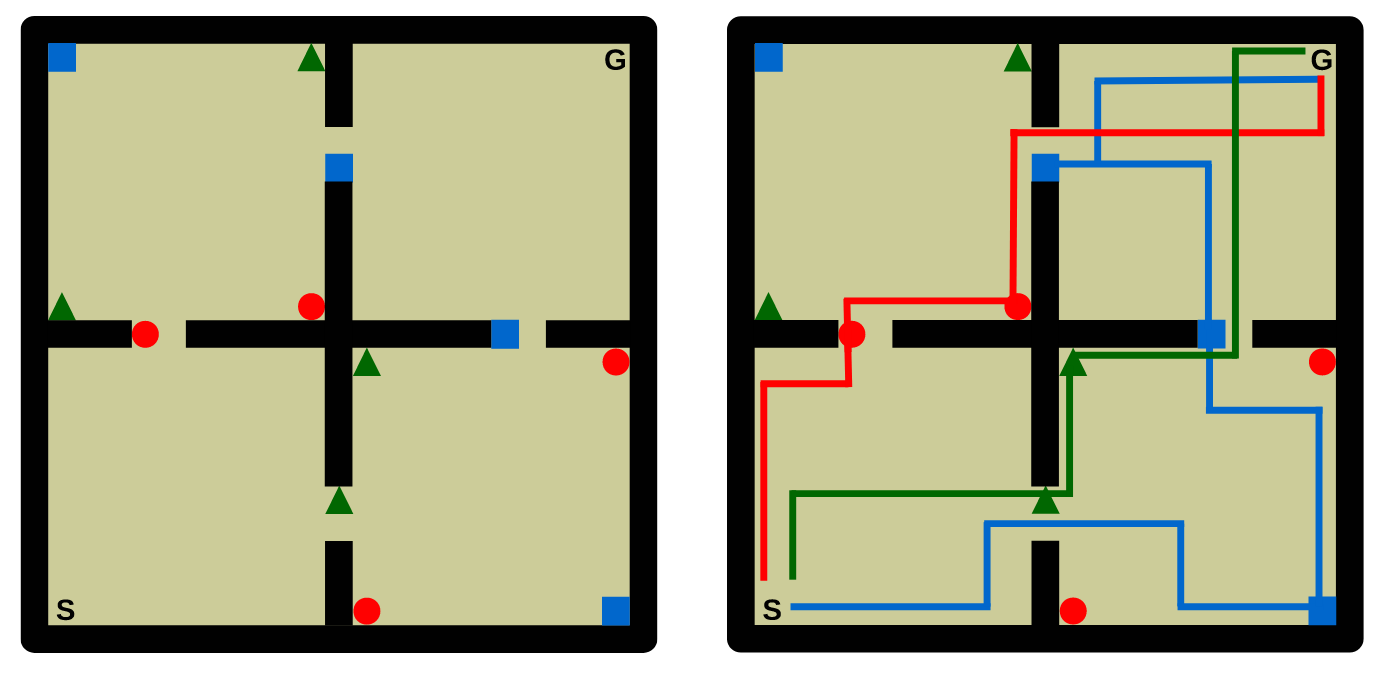
저자들의 첫 번째 실험 환경은 2차원 연속 공간의 네 개 방으로 구성된 네비게이션 환경이다. 에이전트는 한 방에서 시작해 가장 멀리 떨어진 방에 위치한 목표 지점(goal)에 도달해야 한다. 환경에는 ‘좋은(good)’ 객체와 ‘나쁜(bad)’ 객체가 있고, 이 객체들을 지나가면서 집을 수 있다. 객체의 클래스는 세 가지이며, 각 클래스에 따라 보상이 주어진다. 에이전트의 목표는 좋은 객체를 수집하고 나쁜 객체는 피하면서 목표 지점까지 도달하는 것이다. 중요한 점은 객체 클래스에 따른 보상이 매 20,000 트랜지션마다 바뀌기 때문에, 보상 구조가 계속 변하는 다수의 태스크로 이루어진다는 것이다. 총 250개의 태스크가 주어지고, 각 태스크의 보상은 $[-1, 1]^3$ 범위에서 균등하게 샘플된다.

figure 1. Environment layout and some examples of optimal trajectories associated with specific tasks. The shapes of the objects represent their classes; ‘S’ is the start state and ‘G’ is the goal.

제안된 방법은 SFQL(Successor Feature Q-learning)로, $\tilde{w}$와 $\tilde{\psi}^{\pi}$를 (보상 근사식과 SF 벨만 방정식에 기반하여) 점진적으로 업데이트하는 방식이다. 보상이 바뀔 때마다 현재의 $\tilde{\psi}^{\pi_i}$를 저장하고 새로운 $\tilde{\psi}^{\pi_{i+1}}$를 학습하기 시작한다. 비교 대상은 기본 Q-learning(QL)과 정책 재사용 기법인 PRQL(Probabilistic Policy Reuse)이다.

여기서는 SFQL의 두 가지 버전이 비교되었다. 하나는 보상을 정확히 예측할 수 있는 피처 $\phi$에 접근할 수 있는 SFQL-ϕ이다. 이 버전은 에이전트가 사전에 정의된 정확한 feature 함수 $\phi$를 알고 있다는 가정하에 작동한다. 다시 말해, 이 $\phi(s, a, s’)$는 보상을 완전히 정확히 설명할 수 있는 feature로, reward function $r(s, a, s’) = \phi(s, a, s’)^\top w$ 를 완전히 복원할 수 있다. 이 경우, SF는 실제 보상 구조에 딱 맞는 정보만을 담게 되므로 이론적으로는 이상적인 조건이다.

다른 하나는 초기 태스크들로부터 데이터를 수집해 $\tilde{\phi} \in \mathbb{R}^h$를 직접 학습한 SFQL-h이다. 이 버전에서는 feature $\phi$를 모른다고 가정하고, Q-learning을 통해 수집한 초반 20개 태스크의 데이터를 바탕으로 피처 $\tilde{\phi} \in \mathbb{R}^h$를 학습한다. 여기서 $h$는 실제 $\phi$의 차원(실험에서는 4차원)과 다를 수 있으며, $\tilde{\phi}$는 다소 부정확하거나 과잉 또는 부족한 차원의 근사 feature일 수 있다. 이 feature 학습은 다중태스크 학습(multi-task learning) 프로토콜에 기반하여 이루어졌고, 이는 Caruana (1997)와 Baxter (2000)가 제안한 방식에 따른 것이다. Figure 2에 따르면, 모든 버전의 SFQL이 PRQL 및 QL보다 우수한 성능을 보였다. 특히 평균 누적 보상(return) 측면에서 SFQL은 PRQL보다 두 배 이상, QL보다 네 배 이상 더 높은 성과를 냈다.

더욱 흥미로운 점은, SFQL-h가 SFQL-ϕ보다 빠르게 좋은 성능을 보이기 시작했다는 것이다. 이는 다소 역설적으로 보일 수 있다. 왜냐하면 SFQL-ϕ는 정확한 feature를 사용하고 있는 반면, SFQL-h는 학습을 통해 근사 feature $\tilde{\phi}$를 사용하기 때문이다. 이 현상의 주요 원인은 $\tilde{\phi}$의 활성화 범위(activation support)에 있다. SFQL-ϕ에서의 $\phi$는 주어진 상태-행동-전이 $(s, a, s’)$ 조합 중 극히 일부에서만 비제로 값을 가지는 sparse feature일 수 있다. 즉, 특정 상황에서만 보상에 기여한다. 반면, 학습된 $\tilde{\phi}$는 대부분의 상태-행동 전이 쌍에 대해 비제로 값을 갖는 더 dense한 피처로 작동한다. 이 말은, Q-learning 방식의 TD 학습에서 $\tilde{\phi}$가 더 풍부한 학습 신호를 제공한다는 뜻이다. 결국 이는 pseudo-reward signal이 더 조밀(dense)하게 퍼져 있어서 학습 속도를 높이는 효과를 낳는다.

figure 2. Average and cumulative return per task in the four-room domain. SFQL-h receives no reward during the first 20 tasks while learning φ ̃ . Error-bands show one standard error over 30 runs.

두 번째 실험 환경은 MuJoCo 물리 엔진을 사용한 로봇 제어 환경으로, “reacher domain”이라 불린다. 두 관절을 가진 로봇 팔을 특정 목표 지점으로 이동시키는 과제다. 총 12개의 태스크가 있지만, 학습은 그 중 4개에 대해서만 수행되며, 나머지 8개는 테스트용 unseen tasks로 남겨진다. 에이전트는 이처럼 경험하지 않은 태스크에서도 성능을 발휘해야 한다.

실험에서는 앞서 제시한 Successor Features 기반 알고리즘을 DQN(Deep Q-Network)에 접목시킨 SFDQN 알고리즘을 제안한다. 이 알고리즘은 SF를 딥러닝 기반으로 확장하여 복잡한 환경에서도 적용할 수 있도록 만든 것이다. 비교 기준으로는 기본 DQN과 SFDQN이 사용되었다. SFDQN에서 사용된 feature vector $\phi_i$는 목표 위치까지의 거리의 음수(negated distances)로 정의된 피처를 사용하며, SF는 신경망을 통해 학습된다. 각 태스크는 one-hot 벡터 $w_t \in \mathbb{R}^{12}$로 주어지며, DQN은 목표 좌표를 입력으로 받는 반면 SFDQN은 $w_t$를 활용한다.

이 실험의 중요한 특징은 모든 전이 경험이 네 개의 SF 함수 $\tilde{\psi}_{\pi_i}$를 동시에 업데이트하는 데 사용된다는 점이다. 이로 인해 한 태스크에서 수집한 경험이 다른 태스크에도 일반화 가능하게 된다. 각 SF는 아래의 GPI (Generalized Policy Improvement) 방식으로 정책에 사용된다:

figure 3. Normalized return on the reacher domain: ‘1’ corresponds to the average result achieved by DQN after learning each task separately and ‘0’ corresponds to the average performance of a randomly-initialized agent (see Appendix B for details). SFDQN’s results were obtained using the GPI policies πi(s) defined in the text. Shading shows one standard error over 30 runs.

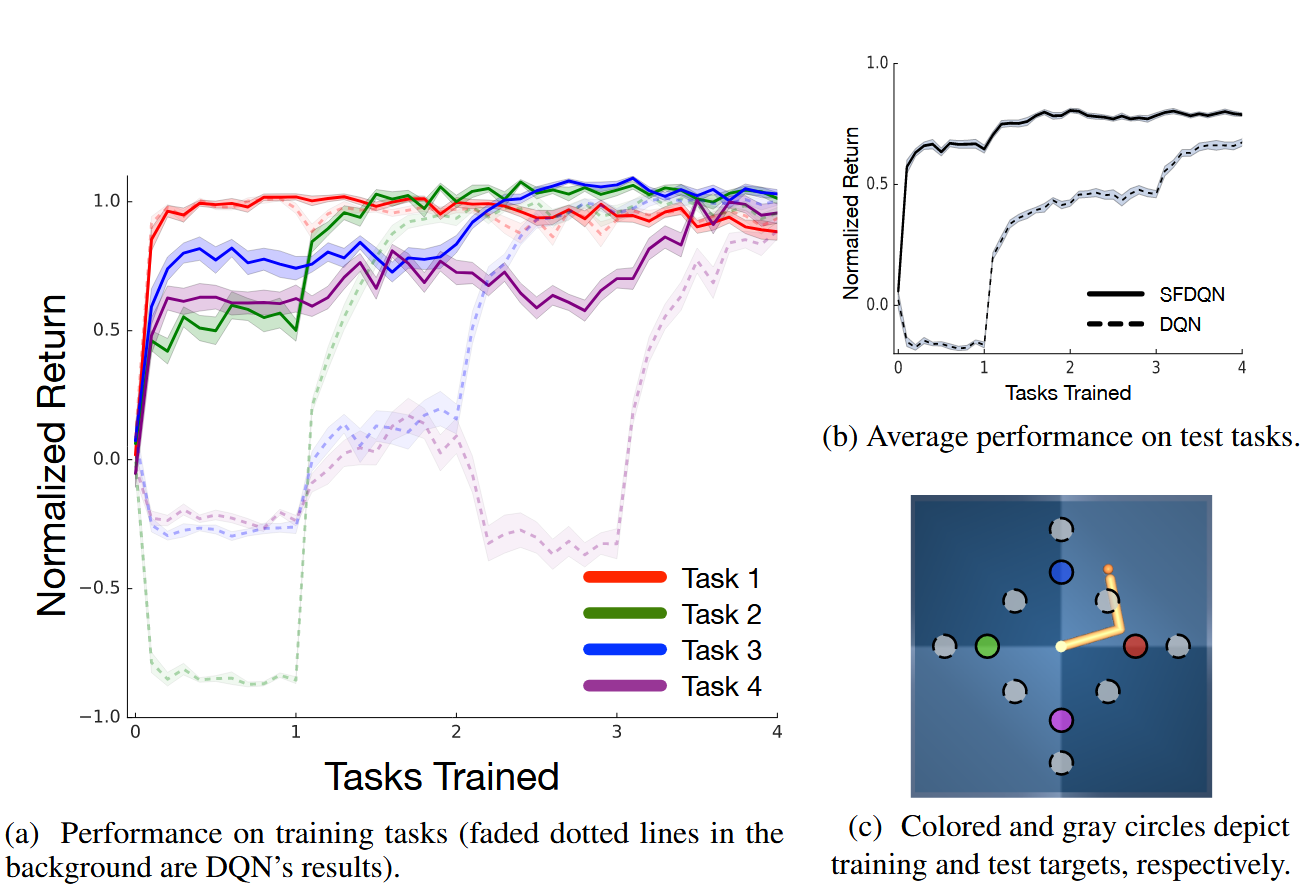
실험 결과는 Figure 3a, 3b에 나타나 있다. 학습 중인 태스크에서 SFDQN은 빠르게 높은 성능에 도달하며, 더 흥미로운 점은 학습하지 않은 테스트 태스크들에서도 성능이 향상된다는 점이다. 이는 SF와 GPI 구조가 경험의 전이를 유도하는 데 효과적이라는 것을 보여준다. 즉, 하나의 태스크에서 학습된 SF가 공유된 dynamics를 바탕으로 다른 태스크의 정책 추정에도 기여할 수 있다.

6. Related work

Barreto 등은 이 논문에서 제안한 방법과 가장 유사한 선행 연구로 Mehta et al. (2012)의 접근을 꼽는다. 그러나 중요한 차이점이 존재한다. Mehta의 연구에서는 feature 벡터 $\phi$와 가중치 벡터 $w$가 항상 환경으로부터 관측 가능한 값으로 주어진다고 가정한다. 또한 평균 보상(average reward)을 기반으로 하는 강화학습 문제를 다루며, 이는 정책 선택이 단 한 번의 결정으로 귀결된다는 점에서 Generalized Policy Improvement(GPI)와는 대조적이다.

이외에도 여러 전이 학습(transfer learning) 알고리즘들이 존재하지만, 특히 기존 정책을 재사용하는 방식으로 이 논문과 관련이 깊은 두 가지 접근법이 있다. 첫째는 실험에 활용된 Fernández et al. (2006)의 Probabilistic Policy Reuse (PPR)이고, 둘째는 Bernstein (1999)의 방법인데, 후자는 매번 새로운 태스크에서 SF를 처음부터 다시 학습하는 방식이다.

Successor Features(SFs)를 단순한 표현 방식으로 본다면, 이들은 Littman et al. (2001)의 Predictive State Representations (PSRs)와 유사한 점이 있다. 다만 PSR은 단일 정책이 아니라 전체 환경의 dynamics를 요약한다는 점에서 차이가 있다. 오히려 SFs는 Inverse Reinforcement Learning에서 사용되는 value function 기반 표현들과 더 유사하다.

또한 SFs는 Sutton et al. (2011)의 General Value Functions (GVFs)와도 관련이 있다. GVFs는 pseudo-reward를 기반으로 하는 확장된 가치 함수로, 이 관점에서 보면 feature $\phi_i$를 pseudo-reward로 보고 SF는 특정 GVF의 한 형태로 해석될 수 있다. 이러한 연결은 두 모델이 공유하는 핵심 철학을 조명한다. 예를 들어 GVF는 “세상의 중요한 지식은 다양한 예측의 형태로 표현될 수 있다”는 가정을 가지며, SFs는 이를 활용하여 어떤 보상 함수든 표현 가능하게 해준다. 반대로 SFs는 어떤 feature $\phi_i$가 유용한지를 선택하는 기준도 제공한다. 즉, 우리가 관심 있는 보상 $r(s,a,s’)$를 근사하는 데 도움이 되는 feature만 필요하다는 점이다.

이와 관련된 또 다른 일반화는 Schaul et al. (2015)의 Universal Value Function Approximators (UVFAs)다. UVFAs는 value function의 입력으로 goal representation을 추가함으로써 전이 학습에 유리한 구조를 제공한다. 이 논문에서 사용하는 식 $\max_j \tilde{\psi}_{\pi_j^*}(s,a)^\top \tilde{w}$ 역시 $(s, a, \tilde{w})$를 입력으로 하는 함수로 해석될 수 있으며, 이는 사실상 UVFA의 구조를 따르는 셈이다. 이 해석은 특히 $\tilde{w}$를 환경 관측값의 함수로 직접 추정할 수 있는 가능성을 시사한다.

마지막으로, SF와 신경망을 결합하려는 시도들도 이전에 존재했다. 예컨대 Kulkarni et al. (2016)과 Zhang et al. (2017)은 SF와 관련된 모듈을 신경망을 통해 공동으로 학습하는 아키텍처를 제안했다. 이들은 GPI를 적용하지는 않았지만, SF를 활용한 전이 학습 측면에서 본 논문과 관련이 깊다. 따라서 이러한 구조들은 이 논문에서 제안한 프레임워크 내에서도 충분히 활용 가능하다.

7. Conclusion

이 논문의 결론에서는 두 가지 핵심 개념이 논의된다. 첫 번째는 Successor Features (SFs)로, 이는 Dayan (1993)의 Successor Representation (SR)을 일반화한 개념이다. SFs는 기존의 이산 상태 공간(discrete space)에서 정의되던 SR을 연속 공간(continuous space)으로 확장하고, 함수 근사(function approximation)를 보다 자연스럽게 적용할 수 있도록 만든다. 두 번째는 Generalized Policy Improvement (GPI)로, 이는 Bellman의 policy improvement를 하나의 정책(policy)이 아닌 복수의 정책들에 대해 일반화한 개념이며, 본문에서 정리 1(Theorem 1)로 공식화되었다.

이 두 개념은 각각 독립적으로도 흥미롭지만, 논문은 이 둘을 결합하여 전이 학습(transfer learning)을 실현하는 데 초점을 맞춘다. 이러한 조합은 동적계획법(Dynamic Programming, DP)의 기본 틀을 확장하면서, 강화학습에서의 전이를 위한 이론적 기반을 제공한다. 이를 보완하기 위해 논문에서는 정리 2(Theorem 2)를 도출하였는데, 이는 유사한 과거의 작업을 경험한 에이전트가 새로운 작업에서도 좋은 성능을 보일 수 있다는 직관을 수학적으로 정형화한 것이다.

이론적 기초 외에도, 본 논문은 다양한 실험들을 통해 SFs와 GPI의 결합이 실제 전이 학습 상황에서 어떻게 효과를 발휘하는지를 실증적으로 보여준다. 저자들은 이 프레임워크가 RL 내에서 전이를 위한 일반적인 틀을 제시하며, 이를 토대로 보다 다양한 태스크를 다룰 수 있는 강력한 에이전트를 구성할 수 있다고 주장한다.