Ten simple rules for the computational modeling of behavioral data - Main article

컴퓨테이셔널 모델링(computational modeling)은 심리학과 신경과학 연구에서 중요한 혁신을 가져왔다. 실험 데이터를 모델에 적합하게 피팅(fitting)하면 행동의 근본적인 알고리즘을 탐구하고, 계산적 변수의 신경학적 상관(neural correlates)을 찾을 수 있으며, 약물, 질병, 중재(intervention)의 영향을 더 깊이 이해할 수 있다. 본 논문에서는 컴퓨테이셔널 모델링을 신중하게 사용하고 의미 있는 통찰을 얻기 위한 10가지 간단한 규칙을 제시한다. 특히, 초보 연구자들이 쉽게 접근할 수 있도록 모델과 데이터를 연결하는 방법을 실용적이고 세부적인 관점에서 설명하고 있다.

“모델이 우리에게 정신(mind)에 대해 정확히 무엇을 말해줄 수 있는가?”라는 핵심 질문을 다루기 위해, 저자들은 가장 기본적인 모델링 기법을 중심으로 설명하며, 실험 코드와 예제를 통해 개념을 구체적으로 보여준다. 그러나 이 논문에서 제시하는 대부분의 규칙은 더 발전된 모델링 기법에도 적용할 수 있다.

1. What is computational modeling of behavioral data?

행동 데이터의 컴퓨테이셔널 모델링(computational modeling of behavioral data)이란 수학적 모델을 이용해 행동 데이터를 보다 체계적으로 이해하는 방법을 의미한다. 행동 데이터는 주로 선택(choice) 형태로 나타나지만, 반응 시간(reaction time), 시선 움직임(eye movement), 신경 활동(neural data) 등의 다양한 관찰 가능한 변수들도 포함될 수 있다. 이 모델들은 실험에서 관찰할 수 있는 자극(stimuli), 결과(outcomes), 과거 경험(past experiences) 등의 변수와 미래 행동을 수학적으로 연결하는 방정식의 형태를 갖는다. 즉, 컴퓨테이셔널 모델은 행동이 생성되는 과정에 대한 ‘알고리즘적 가설(algorithmic hypothesis)’을 구체적으로 구현하는 역할을 한다.

행동 데이터를 ‘이해한다’는 의미는 연구자의 목표에 따라 다를 수 있다. 어떤 경우에는 데이터를 설명할 수 있는 단순한 모델로도 충분하지만, 보다 정량적인 예측을 제공하는 복잡한 모델이 필요한 경우도 있다. 연구자들이 컴퓨테이셔널 모델을 사용하는 주요 목적은 크게 네 가지로 나눌 수 있다.

시뮬레이션(Simulation)

모델의 특정한 매개변수(parameter) 설정하에 가상의 ‘행동 데이터’를 생성하는 과정이다. 이러한 시뮬레이션 데이터를 실제 데이터처럼 분석하면, 행동의 질적 및 양적 패턴을 예측하고 검증할 수 있다. 즉, 시뮬레이션을 통해 이론적 예측을 보다 정밀하게 만들고 실험적으로 검증할 수 있도록 한다.

매개변수 추정(Parameter Estimation)

주어진 모델이 실험 데이터를 가장 잘 설명할 수 있도록 매개변수 값을 찾는 과정이다. 이렇게 얻어진 매개변수는 데이터의 요약 정보로 활용될 수 있으며, 개인차(individual differences)를 연구하거나 약물, 병리적 상태, 실험적 조작(intervention) 등의 영향을 정량화하는 데 사용될 수 있다.

모델 비교(Model Comparison)

여러 개의 가능한 모델 중 어떤 모델이 행동 데이터를 가장 잘 설명하는지를 평가하는 과정이다. 특히, 서로 유사한 질적 예측을 하지만 정량적 차이가 있는 모델들을 비교할 때 유용하다. 모델 비교를 통해 행동을 생성하는 기저 메커니즘을 더 잘 이해할 수 있다.

잠재 변수 추론(Latent Variable Inference)

행동 데이터에서 직접 관찰할 수 없는 숨겨진 변수(latent variable)의 값을 추정하는 과정이다. 예를 들어, 어떤 선택이 주어진 상황에서 얼마나 가치가 있는지(value of choices)와 같은 정보는 직접 측정할 수 없지만, 모델을 통해 추론할 수 있다. 이러한 기법은 특히 신경영상(neuroimaging) 연구에서 활용되며, EEG, ECOG, 전기생리학(electrophysiology), 동공 측정(pupillometry) 등의 다양한 데이터와 결합되어 신경 메커니즘을 밝히는 데 기여한다.

컴퓨테이셔널 모델링은 강력한 도구이지만, 잘못 사용될 경우 잘못된 결론을 도출할 위험이 있다. 시뮬레이션, 매개변수 추정, 모델 비교, 잠재 변수 추론 각각은 특정한 강점과 약점을 가지고 있으며, 부주의하게 다루면 오해를 유발할 수 있다. 따라서 논문에서는 초보자도 이해할 수 있도록 실용적이고 세부적인 접근 방식을 제시하고, 모델을 데이터와 어떻게 연결해야 하는지, 그리고 모델링 과정에서 발생할 수 있는 일반적인 실수를 어떻게 피할 수 있는지를 설명하고자 한다.

이 논문의 목표는 단순히 모델을 구현하는 기술적 측면을 다루는 것이 아니다. 대신, 모델이 인간의 인지 과정과 행동을 어떻게 설명하는지를 보다 심층적으로 탐구하는 데 중점을 둔다. 이를 위해 가장 기초적인 모델링 기법을 중심으로 설명하지만, 논문에서 제시하는 원칙들은 보다 복잡한 모델에도 적용될 수 있다. 또한, 보다 심화된 모델링 기법을 다루는 다양한 튜토리얼, 예제, 그리고 교재들을 참고할 것을 권장한다.

논문에서는 설명의 명확성을 위해 강화학습(reinforcement learning) 모델을 선택하고, 이를 선택 행동(choice data)에 적용하는 예제를 중심으로 설명한다. 이 특정한 도메인을 선택한 이유는 다음과 같다.

1. 강화학습 모델은 학습 과정에 대한 연구에서 특히 인기가 많다.

행동 데이터에서 학습의 특성을 분석할 때, 강화학습 모델은 중요한 도구가 될 수 있다. 특히, 행동 데이터에서 개별적인 시도(trial)는 모든 과거 경험에 영향을 받으며, 이는 고전적인 조건별 데이터 분석(aggregation across conditions)을 어렵게 만든다. 따라서, 컴퓨테이셔널 모델링이 이러한 데이터의 특성을 포착하는 데 유리하다.

2. 학습 과정에서의 연속적 의존성(sequential dependency)은 모델 피팅(fitting) 과정에서 독특한 기술적 문제를 유발한다.

비학습(non-learning) 과제에서는 존재하지 않는 이러한 문제를 다루는 방법을 학습할 필요가 있다.

이 논문에서 다루는 모델링 기법들은 강화학습뿐만 아니라 다른 행동 데이터에도 광범위하게 적용될 수 있다. 예를 들어,

• 반응 시간(reaction time) 모델링 (Ratcliff & Rouder, 1998; Viejo et al., 2015)
• 지각(perception) 및 지각적 의사결정(perceptual decision-making) (Sims, 2018; Drugowitsch et al., 2016)
• 경제적 의사결정(economic decision-making) (van Ravenzwaaij et al., 2011; Nilsson et al., 2011)
• 단기 기억(visual short-term memory) (Donkin et al., 2016)
• 장기 기억(long-term memory) (Batchelder & Riefer, 1990)
• 범주 학습(category learning) (Lee & Webb, 2005)
• 집행 기능(executive functions) (Haaf & Rouder, 2017)

등 다양한 분야에서도 동일한 모델링 원칙이 적용될 수 있다.

2. Design a good experiment!

컴퓨테이셔널 모델링은 강력한 도구이지만, 좋은 실험 설계를 대체할 수는 없다. 모델링은 관찰된 행동을 설명하는 기저 메커니즘을 포착하는 것이 목표이지만, 기본적으로 행동 데이터에 의존하며, 행동 데이터는 실험 설계에 의해 결정된다. 예를 들어, 얼굴 인식(face perception)을 연구하는 사람이 Prospect Theory(전망 이론)를 적용할 수 없고, 손실과 이익의 차이를 연구하려는 연구자가 이익만 제공하는 도박(task with only gains) 실험을 설계하는 것은 의미가 없다. 이러한 단순한 예시에서는 당연해 보이지만, 연구의 복잡성이 증가할수록 적절한 실험 설계를 보장하는 것이 어려워진다.

예를 들어, 특정한 학습 프로토콜이 학습률의 동적 변화(dynamic changes in learning rate), 작업 기억(working memory) 또는 일화 기억(episodic memory)의 기여도를 식별할 수 있을 정도로 충분한 정보를 제공하는가? 보상의 범위(reward range adaptation)를 반영할 수 있는가? 이러한 질문에 대한 답은 실험 프로토콜이 신중하게 설계되지 않는 한 대부분 “아니오”일 것이다.

그렇다면, 컴퓨테이셔널 모델링을 염두에 두고 좋은 실험을 설계하려면 어떻게 해야 할까? 이 과정은 어느 정도 예술적인 감각을 필요로 하지만, 최적의 실험 설계를 위해 고려해야 할 몇 가지 핵심 질문이 있다.

1. 당신이 연구하려는 과학적 질문은 무엇인가?

이 질문은 매우 기본적이지만, 연구를 진행하다 보면 이를 명확하게 정의하지 않고 실험 설계를 하게 되는 경우가 많다.

1. 연구하고자 하는 인지 과정(cognitive process) 은 무엇인가?
2. 어떤 행동적 특성(behavioral aspect) 을 포착하고 싶은가?
3. 어떤 가설(hypothesis) 을 검증하거나 비교하려 하는가?
4. 예를 들어, 실험을 통해 작업 기억이 학습에 어떻게 기여하는지 혹은 행동의 가변성(behavioral variability)이 탐색(exploration)에 어떻게 영향을 미치는지 를 밝히려 한다면, 실험 설계에서 이러한 과정이 드러나도록 해야 한다. 연구 목표를 명확히 설정하면 이후 분석 과정에서 시간을 절약할 수 있다.

2. 실험이 목표로 하는 인지 과정을 실제로 활성화하는가?

이 질문은 단순하지 않으며, 전문가의 의견이나 파일럿 실험(piloting)이 필요할 수도 있다.

1. 실험 설계가 연구하고자 하는 과정(processes) 을 실제로 유발하는가?
2. 단순한 행동 데이터만 수집하는 것이 아니라, 인지적 기전(cognitive mechanisms) 이 반영될 수 있는가?
   예를 들어, 특정한 학습 전략을 연구하고 싶다면, 학습이 일어나는 과정이 실험에서 명확하게 나타나야 한다. 단순한 자극-반응(stimulus-response) 실험이 아니라, 피험자가 전략적으로 학습을 해야 하는 상황이 주어져야 한다.

3. 단순한 데이터 통계(statistics)만으로도 목표로 하는 과정이 확인되는가?

좋은 실험은 컴퓨테이셔널 모델링을 수행하기 전에 이미 특정한 효과를 확인할 수 있어야 한다 (Palminteri et al., 2017). 즉, 모델링 없이도 행동 데이터의 단순한 통계 분석을 통해 연구하고자 하는 과정이 드러나는 것이 이상적이다. 예를 들어, 작업 기억(working memory)의 역할을 연구하려면, 실험 설계에서 기억 부하(memory load)가 변화할 수 있도록 조정해야 한다. 보상 감수성(reward sensitivity)을 연구하려면, 보상의 크기나 빈도에 따라 행동 패턴이 달라지는지를 확인해야 한다. 이렇게 하면, 단순한 행동 분석에서도 인지 과정의 일부가 드러나며, 모델링을 통해 보다 정밀한 분석을 수행할 수 있다. 만약 행동 데이터에서 특정한 효과가 보이지 않는다면, 모델링을 수행하더라도 유의미한 결과를 얻기 어렵다.

4. 실험 설계와 모델 설계는 동시에 이루어져야 한다.

좋은 실험을 설계하는 것은 좋은 모델을 설계하는 과정과 밀접하게 연결되어 있어야 한다. 실험이 특정한 인지 과정과 행동 패턴을 포착할 수 있어야 하고, 모델이 그러한 데이터를 적절히 설명할 수 있어야 한다. 실험 설계를 먼저 완성한 후에 모델을 적용하는 것이 아니라, 초기 단계에서부터 실험과 모델을 함께 설계하는 것이 이상적이다.

5. “나는 실험을 직접 수행하지 않는 모델러인데, 이 과정을 무시해도 될까?”

컴퓨테이셔널 모델링 연구자 중에는 실험을 직접 수행하지 않고, 기존의 출판된 연구 결과나 공개 데이터셋(public dataset)을 분석하는 경우도 많다. 이러한 모델러들은 실험 설계에 대해 신경 쓰지 않아도 된다고 생각할 수도 있다. 그러나 저자들은 이에 동의하지 않는다. 모델러들도 자신의 모델을 검증할 수 있는 더 나은 실험이 가능할지 고민해야 하고, 모델이 적용될 수 있는 실제 행동 데이터가 어떤 특성을 가지는지 파악해야 한다. 이러한 사고 방식은 모델을 보다 구체적이고 실질적으로 만들며, 모델이 적용될 수 있는 범위를 넓혀줄 수 있다. 특히, 실험을 직접 수행하는 연구자들과 협력하면, 모델이 현실적인 데이터에 더 적합하게 조정될 수 있으며, 새로운 통찰을 얻을 수 있다.

마지막으로, 실험 설계에 대한 구체적인 아이디어를 제안하면, 실험을 수행하는 연구자들이 실제로 그 실험을 실행하도록 설득할 수 있는 가능성도 높아진다. 연구를 발전시키기 위해서는 모델러와 실험 연구자 간의 협력이 필수적이다.

Design good models

1. 모델링의 목적을 명확히 하라

모델을 설계할 때 가장 중요한 것은 모델을 사용하는 이유를 명확히 하는 것이다.

1. 설명적 모델(Descriptive model)

행동 데이터를 요약하는 것이 목적 예: 반응시간 분포를 단순한 수학적 공식으로 요약하는 모델

1. 기계론적 모델(Mechanistic model)

행동과 뇌의 메커니즘을 연결하는 것이 목표 예: 신경과학에서 보상 학습과 도파민 신호를 연결하는 강화학습 모델

1. 개념적 모델(Conceptual model)

특정 이론적 개념을 수학적으로 표현하는 것이 목적 예: 강화학습 이론에서 탐색(exploration)과 활용(exploitation) 간 균형을 설명하는 모델

Kording et al. (2018)에 따르면, 컴퓨테이셔널 모델링 연구자들은 매우 다양한 목표를 가지고 있으며, 자신이 어떤 목표를 가지고 모델링을 수행하는지 명확히 아는 것이 가장 중요하다.

2. 모델을 설계하는 다양한 접근법

컴퓨테이셔널 모델을 설계하는 방법은 여러 가지가 있으며, 연구 목적에 따라 적절한 방법을 선택할 수 있다.

1) 휴리스틱 기반 접근법 (Heuristic Approach)

단순한 규칙을 사용하여 특정 행동을 설명하는 모델을 설계하는 방법이며, 경험을 통해 행동이 어떻게 변화하는지 간단한 방식으로 설명한다.

예시: 델타 학습 규칙(Delta rule)

\[ΔV = α (R - V)\]

Rescorla-Wagner 모델(Rescorla & Wagner, 1972)에서 사용되었다.

2) 인공지능 및 수학적 알고리즘을 참고하는 접근법

인공지능(AI), 컴퓨터 과학, 응용 수학 분야에서 사용되는 알고리즘을 참고하여 인간의 행동을 설명하는 모델을 구축하며, 인간과 동물의 행동 및 신경 기제를 설명하는 데 사용되었다.

예시: 강화학습 모델(Reinforcement Learning) - Q-learning (Watkins & Dayan, 1992), Temporal Difference Learning (Sutton & Barto, 2018)

3) 베이즈 최적 모델 (Bayes-optimal Models)

환경과 과제에 대한 최적의 해결책을 찾는 모델을 설계하며, 인지 과정이 최적의 방식으로 작동하는지를 테스트하는 데 유용하다. 보다 현실적인 모델을 만들기 위해, 제약 조건(bounded rationality constraints) 을 추가할 수도 있다.

예시: 이상적 관찰자 모델(Ideal Observer Model) 시각 인지 연구에서 자극을 최적적으로 처리하는 방법을 설명하는 모델 (Geisler, 2011) 계산 자원의 한계를 고려하는 모델 (Lieder et al., 2018)

3. 좋은 모델을 만들기 위해 지켜야 할 원칙

모델을 설계할 때 다음 세 가지 원칙을 따라야 한다.

1. 모델은 최대한 단순해야 하지만, 너무 단순해서는 안 된다.

아인슈타인의 명언:
“Everything should be made as simple as possible, but not simpler.”

단순한 모델은 적합(fitting)이 쉽고 해석이 용이하다. 과도하게 복잡한 모델은 데이터를 잘 설명하는 것처럼 보일 수 있지만, 실제로는 과적합(overfitting) 문제를 초래할 가능성이 크다. 모델 비교 기법(model comparison techniques) 은 과적합을 방지하기 위해 과도하게 복잡한 모델에 패널티를 부여한다(자세한 내용은 Appendix 2 참고).

1. 모델은 해석 가능해야 한다.

모델이 행동 데이터를 잘 설명한다고 하더라도, 해석할 수 없는 모델은 유용하지 않다. 예를 들어서, 강화학습 모델에서 음의 학습률(negative learning rate) 은 논리적으로 해석하기 어렵다. 의미 없는 매개변수가 모델에 포함될 경우, 이는 단순히 모델이 중요한 요소를 놓치고 있음을 나타낼 수도 있다. 따라서 모델의 각 요소가 의미 있는 방식으로 행동 데이터를 설명할 수 있어야 한다.

1. 모델은 연구자가 테스트하고자 하는 모든 가설을 포착할 수 있어야 한다.

특정한 가설만 고려하는 모델을 만들면, 모델 비교(model comparison)를 수행할 때 제한적일 수 있다. 덧붙여서, 가설을 검증하는 데 사용되는 모델만이 아니라, 경쟁 가설(competing hypotheses)을 반영할 수 있는 모델도 포함해야 한다. 예를 들어서 기본 모델이 랜덤한 행동을 하는 모델이고, 가설 모델 (Hypothesis Model)이 연구자가 검증하려는 학습 모델이라면 학습이 아닌 다른 메커니즘으로 행동을 설명하는 대조 모델 (Competing Model)이 있으면 좋다는 것이다. 연구자가 선호하는 특정 모델에 너무 의존하지 않고, 데이터가 가장 적절한 모델을 선택하도록 해야 한다.

Simulate, simulate, simulate!

이 부분에서는 모델링을 이용한 행동 실험 분석에서 시뮬레이션(Simulation)의 중요성을 강조하고 있다. 실험 설계와 계산 모델이 정해진 후, 가장 중요한 단계 중 하나는 가짜 데이터(surrogate data)를 생성하는 것이다. 이를 통해 모델이 실험 데이터를 얼마나 잘 설명하는지 검증하고, 모델과 실험 설계를 조정할 수 있다. 이를 위해 다음과 같은 구체적인 단계를 거친다.

1. 모델 독립적인 측정값을 정의하기 (Define Model-Independent Measures)

모델을 검증하기 위해서는 특정 모델에 의존하지 않는 행동 측정값(model-independent measures)을 정의해야 한다. 이는 왜 중요한가? 실험에서 질적(qualitative) 특징을 찾고, 이러한 측정값을 통해 시뮬레이션 데이터와 실제 데이터를 비교할 수 있기 때문이다. 예를 들어 강화 학습 모델을 테스트할 경우, 피드백에 대한 반응률, 선택 반복성, 학습 속도 등이 모델 독립적인 측정값이 될 수 있다. 이를 통해 시뮬레이션 데이터에서 어떤 행동 패턴이 나오는지 먼저 확인한 후, 실제 실험 데이터에서도 동일한 패턴을 찾을 수 있는지 분석한다.

2. 모델을 다양한 파라미터 값에 대해 시뮬레이션하기 (Simulate the Model Across the Range of Parameter Values)

모델의 대부분은 자유 파라미터(free parameters)를 가지고 있으며, 이 값이 변하면 행동도 달라진다. 따라서, 모델의 모든 자유 파라미터에 대해 광범위한 값을 설정하고, 이를 통해 시뮬레이션을 수행한다. 이후 각 파라미터 값에 따라 행동이 어떻게 변화하는지 시각적으로 확인한다. 이 과정에서 파라미터가 어떤 방식으로 행동을 조절하는지 직관적으로 이해하고, 개별 참가자 간의 차이를 설명하기 위한 파라미터 해석이 가능하다.

예를 들어, 확률적 강화 학습(probabilistic reinforcement learning)에서 Rescorla-Wagner 모델(Model 3, Equation 3)을 적용할 경우 \(\alpha\) (학습률, learning rate)는 학습 속도 및 안정적인 행동 여부에 영향을 주며, \(\beta\) (inverse temperature)는 선택이 얼마나 결정적(deterministic)인지 또는 랜덤(random)한지를 조절한다.

figure 1. Simulating behavior in the two-armed bandit task.

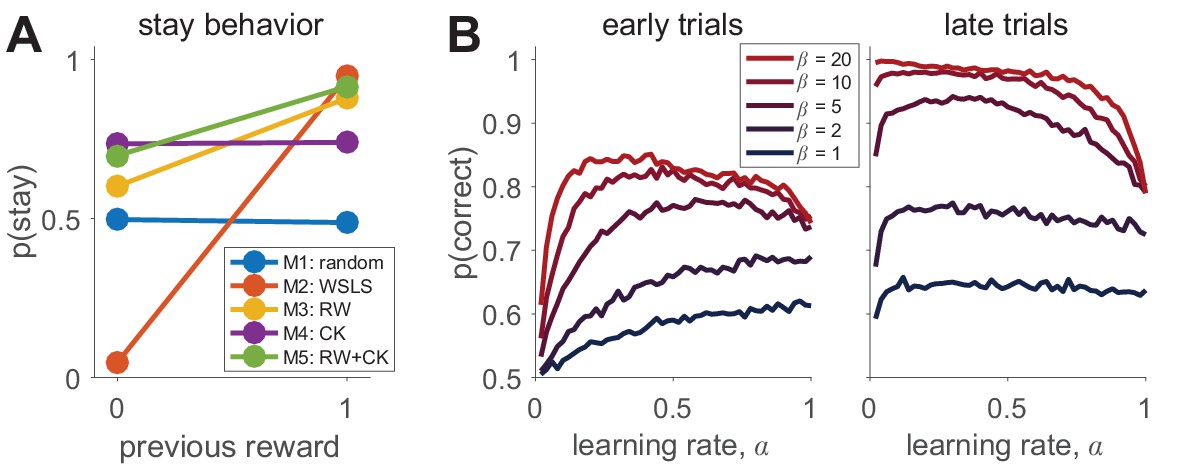
강화 학습 모델에서 파라미터 분석을 하는 사례에서 \(\alpha\) 가 높으면 새로운 정보에 빠르게 반응하고, 낮으면 점진적인 학습을 보인다. \(\beta\) 가 낮으면 행동이 무작위에 가깝고, 높으면 보상 기대값이 높은 선택지를 확실하게 고른다. 이를 그래프로 표현하면, 파라미터 값 변화에 따른 행동의 차이를 직관적으로 확인할 수 있다(Box 2—figure 1B 참조).

3. 서로 다른 모델의 시뮬레이션된 행동을 시각화하기 (Visualize the Simulated Behavior of Different Models)

서로 다른 모델이 질적으로 다르게 행동을 예측하는지 확인하는 것이 중요한데, 그 이유는 서로 다른 모델이 비슷한 예측을 한다면, 실험에서 모델을 구분하기 어렵기 때문이다. 실험은 모델을 명확하게 구별할 수 있도록 설계되었는지 검증하는 과정이 되어야 한다. 예를 들어, 강화 학습 모델과 선택 경향성(Choice Kernel) 모델이 동일한 데이터를 설명할 수 있다면, 추가적인 실험 조건이 필요할 수 있다.

Box 2—figure 1A에서 다양한 모델이 실험 조건에서 어떻게 다른 행동을 예측하는지를 확인할 수 있다. 만약 여러 모델이 동일한 패턴을 예측한다면, 더 나은 실험 설계를 찾아야 한다.

4. 시뮬레이션의 일반적 목표 (General Goal of Simulation)

전체적으로 시뮬레이션의 목표는 모델과 실험 설계가 연구 목표를 충족하는지 검증하는 것이다. 이 때 다음과 같은 질문을 생각해 볼 수 있다. 실험이 기대하는 행동을 충분히 유발할 수 있는가? / 모델의 파라미터가 행동을 해석할 수 있도록 설계되었는가? / 서로 다른 모델이 구별 가능한 예측을 제공하는가? 이 질문들에 대한 답이 “Yes” 라면, 다음 단계(모델 피팅)로 진행할 수 있다. 그렇지 않다면, 실험 설계 및 모델을 다시 조정하는 과정(Iteration)이 필요하다.

Fit the parameters

이 부분에서는 계산 모델의 핵심적인 과정 중 하나인 모델의 파라미터를 피팅(fitting) 하는 방법을 설명하고 있다. 즉, 행동 데이터를 가장 잘 설명하는 모델의 파라미터 값을 어떻게 찾을 것인가? 에 대한 논의이다. 여기서는 최대 우도 추정(Maximum Likelihood Estimation, MLE) 을 중심으로 다루지만, Markov Chain Monte Carlo(MCMC)와 같은 다른 방법도 존재한다. MLE는 모델의 파라미터 값이 주어진 데이터에서 실제로 관측된 행동을 최대한 잘 예측하도록 하는 값을 찾는 방식이다.

1. 최대 우도 추정 (Maximum Likelihood Estimation, MLE)

MLE의 목표는 주어진 데이터 \(d_{1:T}\) 에 대해 모델 \(m\) 의 파라미터 \(\theta\) 를 찾는 것이다. 즉, 데이터가 발생할 확률(우도, likelihood)을 최대화하는 파라미터 값을 찾는다.

우도 함수 (Likelihood Function)는 데이터 \(d_{1:T}\) 가 주어졌을 때, 모델 \(m\) 의 파라미터 \(\theta\) 가 존재할 확률을 나타낸다. 이를 \(p(d_{1:T} \mid m, \theta)\) 라고 표현한다. 우도 함수는 0과 1 사이의 작은 값들의 곱이므로, 연산 과정에서 0으로 수렴하는 문제가 발생할 수 있다. 따라서 로그를 취한 로그-우도 함수 를 사용하면 계산이 훨씬 안정적이고 tractable 해진다.

\[LL = \log p(d_{1:T} \mid m, \theta) = \sum_{t=1}^{T} \log p(c_t \mid d_{1:t-1}, s_t, m, \theta)\]

여기서, \(p(d_{1:T} \mid m, \theta)\)은 주어진 과거 정보와 모델 파라미터 하에서 각 선택이 발생할 확률을 의미한다. 이 확률을 최대화하는 \(\theta\) 를 찾는 것이 목표이다.

2. 최대 우도 추정의 실제 적용

이론적으로는 로그-우도 함수를 최대화하는 \(\theta\) 를 찾는 것이 간단해 보이지만, 실제로 이는 매우 어렵기 때문에 최적화(Optimization) 알고리즘을 이용해야 한다.

2.1 브루트 포스 탐색 (Brute Force Search)

가능한 모든 \(\theta\) 값을 하나씩 대입하여 로그-우도를 계산하고, 가장 큰 값을 선택하는 방식이다. 단순한 경우 (예: 파라미터가 1~2개 정도일 때)에는 사용할 수 있지만, 파라미터 공간이 커지면 연산량이 너무 커지므로 현실적으로 불가능하다.

2.2 경사 상승법 (Gradient Ascent)

\(LL\) 을 직접 미분하여 기울기를 계산하고, 기울기가 가장 큰 방향으로 파라미터를 조정하는 방법이나, 실제로는 \(LL\) 을 미분하기 어려운 경우가 많아, 수치적 최적화 기법이 사용된다.

2.3 수치적 최적화 기법

최적화를 빠르고 효율적으로 수행하기 위해 다양한 수치적 최적화 알고리즘이 존재한다. 예시로 Matlab의 fmincon 함수는 다양한 최적화 알고리즘 (예: More & Sorensen, 1983; Byrd et al., 2000)을 제공한다. fmincon 은 기본적으로 최소화 알고리즘이므로 -LL을 최소화하면 LL을 최대화하는 것과 동일한 효과를 얻을 수 있다. 또한 Python의 scipy.optimize 패키지에서도 유사한 기능을 제공하며, scipy.optimize.minimize() 함수 등을 사용할 수 있다. R의 optim 함수에서도 비슷한 방식으로 로그-우도를 최적화할 수 있다.

3. MLE 적용 시 주의할 점

MLE를 수행하는 과정에서 다양한 수치적 문제(numerical issues)가 발생할 수 있다. 이를 방지하기 위한 몇 가지 팁을 소개한다.

3.1 초기값 설정 문제 (Initial Conditions and Finite Log-Likelihoods)

최적화 알고리즘은 초기값(initial parameter values) 을 설정해야 하는데, 초기값이 잘못 설정되면 로그-우도가 NaN 또는 \infty 가 되는 경우가 발생할 수 있다. 따라서 합리적인 초기값을 설정하는 것이 중요하다.

3.2 연산 오류 (Rounding Errors, Zeros, and Infinities)

\(p(c_t \mid d_{1:t-1}, s_t, m, \theta)\) 가 0이 되면 로그-우도가 \infty 로 발산할 수 있다. 반대로, exp() 연산에서 너무 큰 값이 들어가면 \infty 가 나올 수도 있다. 이를 방지하기 위해 모델의 파라미터 범위를 적절히 조정하고, 작은 값을 추가하는 방식(e.g., log(x + \epsilon))을 사용할 수 있다.

3.3 파라미터 제약 설정 (Parameter Constraints)

파라미터가 논리적으로 불가능한 값으로 설정되지 않도록 제약을 둬야 한다. 예를 들어, 학습률 \(\alpha\) 는 \(0 \leq \alpha \leq 1\) 범위를 가져야 한다. 만약 제약을 설정하지 않으면 \(\alpha > 1\) 같은 비현실적인 값이 나올 수 있다.

3.4 지역 최소값(Local Minima) 문제

대부분의 최적화 알고리즘은 전역 최적해(global optimum)를 보장하지 않고, 지역 최적해(local optimum)만 찾는다. 즉, 어떤 초기값에서는 최적해를 찾았다고 생각했지만, 더 좋은 값이 존재할 수 있다. 이를 보완하기 위해서는 여러 개의 랜덤 초기값을 설정하여 최적화를 여러 번 실행하거나, 최적화 결과를 비교하여 가장 높은 로그-우도를 반환하는 결과를 선택하거나, 최적화 횟수를 늘려서 충분한 탐색을 수행할 수 있다.

또한 최적화가 잘 수행되었는지 확인하기 위해 로그-우도 값이 수렴하는지 확인해야 한다. 랜덤 초기값 개수에 따른 로그-우도 변화 그래프를 그려서 최적해에 수렴하는지 시각적으로 확인할 수도 있다. 파라미터 복원이란, 모델이 실제로 올바른 파라미터를 찾을 수 있는지를 확인하는 과정이다. 이 과정의 핵심 아이디어는 가짜 데이터(fake data)를 생성한 후, 이를 다시 분석하여 원래 사용된 파라미터 값을 정확히 복원할 수 있는지 확인하는 것이다.

Check that you can recover your parameters

모델의 파라미터 피팅(parameter fitting)을 신뢰할 수 있는지 검증하는 방법인 “파라미터 복원(Parameter Recovery)” 과정에 대해 설명하고 있다. 즉, 최적화 과정을 통해 얻은 최적의 파라미터 값들이 실제 데이터를 잘 반영하는지 확인하는 필수적인 과정이다. 이 과정이 중요한 이유는 MLE(최대 우도 추정)로 찾은 파라미터 값이 의미 있는지 검증하기 위해서이며, 실험 데이터를 해석하기 전에, 모델이 제대로 동작하는지 확인할 수 있다는 장점도 있다. 또한 모델이 특정 조건에서만 잘 작동하는지(예: 특정 파라미터 범위에서만 신뢰할 수 있는지), 또는 모델이 특정 실험 데이터에 대해 신뢰할 만한 결과를 제공하는지 검토할 수 있다.

파라미터 복원의 절차는 다음과 같이 간단한 3단계로 이루어진다.

먼저, 알려진 파라미터 값(‘참값’)을 사용하여 모델을 이용해 가짜 데이터를 생성한다. 이때 실제 실험과 동일한 조건에서 데이터를 생성해야 한다. 예를 들어, \(\alpha = 0.2\), \(\beta = 5\) 등의 특정 파라미터 값으로 데이터를 생성한 후, 모델을 이용해 참가자의 선택 행동을 시뮬레이션한다. 이렇게 하면, 우리가 알고 있는 정답(ground truth)이 존재하는 가짜 데이터셋이 만들어진다.

이제, 앞서 생성한 가짜 데이터에 대해 최적화(optimization)를 수행하여 파라미터를 다시 추정한다. 즉, MLE(Maximum Likelihood Estimation) 등의 방법을 이용해 모델을 데이터에 맞추고, 그 과정에서 얻어진 최적의 파라미터 값(추정된 \(\alpha\) 및 \(\beta\) 값)을 저장한다. 이 단계에서는 파라미터 복원이 얼마나 정확하게 이루어지는지를 평가하기 위해 다양한 초기값을 사용하여 최적화를 여러 번 반복하는 것이 중요하다.

마지막으로, 모델이 복원한 파라미터 값들이 처음 가짜 데이터를 생성할 때 사용한 값들과 얼마나 일치하는지 확인한다. 이론적으로는 완벽한 모델이라면 원래 사용한 파라미터 값과 복원된 파라미터 값이 완전히 일치해야 한다. 그러나 실제로는 다양한 이유(최적화 오류, 데이터 부족, 모델의 근본적 한계 등)로 인해 완벽한 복원이 어려울 수 있다.

파라미터 복원 과정에서 고려해야 할 사항

적절한 파라미터 범위 선택

파라미터 복원을 수행할 때에는, 어떤 범위의 파라미터 값을 사용할지 결정하는 것이 중요하다. 모델이나 실험에 따라 특정 범위의 파라미터 값에서만 신뢰할 만한 복원이 가능할 수 있다.

예를 들어, Softmax 파라미터 \(\beta\) 값이 너무 크면, 거의 항상 같은 선택을 하게 되어 모델이 이를 복원하기 어려워진다. 따라서, 너무 큰 \(\beta\) 값에서는 복원이 어려울 수 있다. 만약 실험 데이터를 이미 분석한 경우라면, 실험 데이터를 피팅한 결과 얻은 파라미터 값의 범위를 기반으로 설정하면 된다. 만약 모델이 기존 연구에서 사용된 경우, 기존 연구에서 사용된 파라미터 범위를 참고하여 설정할 수 있다. 모델이 새로운 경우라면, 가능한 한 넓은 범위에서 파라미터를 샘플링하여, 어느 범위에서 복원이 잘 되는지 확인한다. 이 과정에서 모델의 특정 파라미터가 실제 데이터 분석에서 사용될 범위에서만 신뢰할 수 있는지 평가하는 것이 중요하다.

시뮬레이션된 값과 복원된 값의 상관관계 분석

파라미터 복원이 잘 이루어졌는지 평가하는 가장 간단한 방법은 복원된 값과 원래 값 사이의 상관관계를 계산하는 것이다. 즉, 모델이 정확한 파라미터 값을 예측할 수 있는지를 정량적으로 평가할 수 있다. 완벽한 모델이라면 시뮬레이션된 값과 복원된 값이 완전히 일치하는 1:1 직선 관계를 나타내야 한다. 만약 상관관계가 낮거나 특정 방향으로 치우친다면, 이는 모델이 특정 파라미터를 신뢰할 수 없는 방식으로 복원하고 있을 가능성이 있다. 따라서, 단순한 상관계수(correlation coefficient)뿐만 아니라, 실제로 산점도(scatter plot)를 그려서 관계를 시각적으로 확인하는 것이 중요하다.

복원된 파라미터 간의 상관관계 확인

또한, 복원된 파라미터들 간의 상관관계를 분석하는 것도 중요하다. 만약 서로 독립적인 두 개의 파라미터가 실제로는 강한 상관관계를 보인다면, 이는 두 파라미터가 모델 내에서 서로 상쇄(trade-off)하고 있을 가능성이 높다.

Daw (2011)의 연구 결과를 예제로 보면, 특정 모델에서 \(\alpha\) 와 \(\beta\) 가 강한 음의 상관관계를 보이면, 실제로는 하나의 파라미터만이 데이터를 설명하고 있는 것이고, 다른 파라미터는 불필요할 수도 있다. 이러한 문제를 해결하기 위해 모델을 다시 매개변수화(reparameterization)하거나 실험 설계를 변경해야 할 수도 있다.

파라미터 비교 연구에서의 활용

최근 계산 모델링 연구에서는 파라미터 값을 비교하여 그룹 간 차이를 분석하는 연구가 많다. 예를 들어, 정신 질환 연구에서는 조현병 환자 vs 건강한 참가자의 학습률 \(\alpha\) 차이 분석 (Collins et al., 2014)을 분석하거나 신경과학 연구에서는 특정 뇌 영역을 자극할 때 파라미터 변화 관찰 (Zajkowski et al., 2017)하는 등의 연구이다. 이러한 연구를 수행하기 전, 파라미터 복원 과정을 통해 실제로 그룹 차이를 검출할 수 있는지 평가하는 것이 필수적이다. 즉, 실제로 그룹 간 차이가 존재하는 데이터를 생성한 후, 모델이 이를 올바르게 복원할 수 있는지 검증하여 연구의 통계적 검출력(statistical power)을 미리 평가할 수 있다.

Can you arbitrate between different models?

이 부분에서는 여러 모델 중에서 어떤 모델이 주어진 데이터를 가장 잘 설명하는지 결정하는 방법, 즉 실험 데이터를 설명하는 여러 모델이 있을 때, 가장 적절한 모델을 선택하는 과정을 설명한다. 모델 비교의 궁극적인 목표는 주어진 데이터 \(d_{1:T}\) 가 여러 모델 중 어떤 모델에서 생성되었을 가능성이 가장 높은지를 평가하는 것이다. 이를 위해, 각 모델에 대한 데이터 적합도(fit)를 계산하고, 이를 비교하여 가장 적절한 모델을 선택한다. 가장 직관적인 모델 비교 방법은 각 모델의 로그-우도 값(log-likelihood, \(\log p(d_{1:T} \mid m, \theta)\))을 비교하여, 로그-우도가 가장 큰 모델을 선택하는 것이다. 그러나, 모델을 평가할 때 사용한 데이터(\(d_{1:T}\))와 모델을 학습할 때 사용한 데이터가 동일하다면, 이는 과적합을 초래할 수 있다.

만약 매 선택마다 새로운 파라미터를 도입하는 모델이 있다고 가정하자. 이 모델은 단순히 실험 참가자가 실제로 선택한 선택지를 그대로 기억하여 완벽하게 예측할 수 있다. 즉, 로그-우도 값이 가장 높지만, 실제로는 미래의 새로운 데이터에 대해 아무런 일반화 능력을 가지지 않는다. 이 모델은 데이터를 설명하는 것이 아니라 단순히 데이터를 암기하는 것에 불과하므로, 의미 있는 해석을 제공하지 않는다.

모델이 데이터에 너무 맞춰져 있으면, 대개 새로운 데이터에 대해 일반화할 수 있는 능력이 저하되므로 파라미터가 많은 복잡한 모델이 항상 더 좋은 모델은 아니다. 이 문제를 해결하기 위해, 모델의 자유도(degrees of freedom, 즉 사용된 파라미터 수)를 고려하는 방법이 필요하다. 그중 가장 간단한 방법이 베이지안 정보 기준(Bayesian Information Criterion, BIC)이다.

과적합을 방지하는 모델 비교 방법: BIC (Bayesian Information Criterion)

BIC는 로그-우도를 기준으로 하되, 모델이 사용하는 파라미터 수에 패널티를 부과하는 방식이다. 즉, 모델이 데이터를 얼마나 잘 설명하는지를 평가하면서, 동시에 불필요하게 많은 파라미터를 사용하는 모델을 불리하게 만든다.

\[BIC = -2 \log L + k_m \log(T)\]

위는 BIC의 정의이며, \(\log L\)은 모델의 최적화된 로그-우도(log-likelihood) 값, \(k_m\)은 모델 \(m\) 이 가지는 자유 파라미터(free parameters)의 개수, \(T\)은 데이터 포인트(샘플 수, trials) 개수를 의미한다. BIC의 원리는 간단하다. 로그-우도가 높을수록 (\(-2 \log L\) 값이 작을수록) 모델이 데이터를 잘 설명한다고 간주하나, 파라미터 수(\(k_m\))가 많으면, BIC 값이 커지는 패널티를 부과한다. 따라서, BIC 값이 작을수록 좋은 모델로 간주한다. 즉, BIC는 모델의 적합도를 평가하면서도, 불필요한 복잡성을 줄이는 방식이다.

모델 비교의 검증: 모델 복원 (Model Recovery)

BIC와 같은 모델 비교 방법을 사용하기 전에, 이 방법이 실제로 신뢰할 수 있는지를 검증해야 한다. 이를 위해 수행하는 과정이 모델 복원(Model Recovery) 이다.

모델 복원의 기본 아이디어는 다음과 같다. 먼저 여러 개의 후보 모델(A, B, C 등)에서 가짜 데이터(fake data)를 생성한다. 이후 각 모델로 생성된 데이터를 다시 모델에 피팅하여, 어떤 모델이 가장 잘 적합하는지 확인한다. 이 과정에서, 데이터를 생성한 모델이 다시 정확하게 선택되는지를 평가한다. 이 과정을 통해, 모델 비교 방법이 실제로 모델을 잘 구별할 수 있는지 검증할 수 있다. 결과는 혼동 행렬(confusion matrix) 을 사용하여 시각적으로 표현할 수 있다.

이상적인 경우, 혼동 행렬은 단위 행렬(identity matrix)처럼 나타나야 한다. 즉, 모델 A가 생성한 데이터는 모델 A가 가장 잘 적합해야 하고, 모델 B가 생성한 데이터는 모델 B가 가장 잘 적합해야 한다. 만약 혼동 행렬에서 오차(off-diagonal elements)가 크다면, 모델 복원이 잘 이루어지지 않았다는 의미이며, 모델 비교 방법이 신뢰할 수 없을 수 있다.

모델 비교에서 주의할 점

BIC 이외에도 Akaike Information Criterion (AIC) 과 같은 다른 모델 비교 방법이 존재한다. 각 방법은 자유 파라미터의 영향을 다르게 처리하므로, 비교 결과가 달라질 수 있다. 따라서, 혼동 행렬을 확인하여 어떤 모델 비교 방법이 더 신뢰할 수 있는지를 검증하는 것이 중요하다.

또한 모델 복원 성능은 사용한 파라미터 값의 범위에 따라 달라질 수 있다. 특정 범위에서는 두 모델이 구별되지만, 일부 파라미터 값에서는 두 모델이 매우 유사한 예측을 할 수도 있다. 따라서, 실험 데이터에서 얻어진 파라미터 범위를 기반으로 모델 복원을 수행하는 것이 중요하다.

Run the experiment and analyze the actual data

이 부분에서는 이전 단계에서 시뮬레이션과 파라미터/모델 복원 과정을 통해 모델과 실험 설계가 잘 작동하는지 검증한 후, 이제 실제 피험자의 행동 데이터(empirical data)를 대상으로 모델 기반 분석을 수행하는 과정을 설명한다. 우선, 모델을 피팅하기 전에 모델 독립적인 분석(model-independent analysis)을 통해서 데이터에서 기대했던 패턴이나 가설에 부합하는 행동이 나타나는지 확인하는 것이 매우 중요하다. 만약 이러한 분석에서 기대한 결과가 나타나지 않는다면, 모델을 피팅하는 것은 의미가 없으며, 실험 설계나 연구 질문 자체를 재검토해야 한다.

실제 데이터 분석 단계에서는 먼저 모델 독립적인 분석을 수행한다. 이는 시뮬레이션 단계에서 설정한 가설에 따른 행동 패턴(예: 보상에 따른 선택의 변화, 학습 속도 등)을 데이터에서 직접 확인하는 것이다. 만약 모델 독립적인 분석 결과가 긍정적이라면, 그 다음 단계로 이전에 개발한 모델들을 피팅하고, 모델 간 비교(model comparison)를 수행한다. 모델 피팅에서는 최대 우도 추정(MLE)이나 기타 최적화 기법을 사용하여 데이터에 가장 잘 맞는 파라미터 값을 찾게 된다. 이후 모델 비교에서는 BIC와 같은 기준을 사용하여, 과적합 문제를 고려하면서 여러 모델 중 어떤 모델이 데이터를 가장 잘 설명하는지를 판단한다.

피팅한 후에는, 시뮬레이션 단계에서 수행했던 파라미터 복원과 모델 복원 실험을 통해 검증한 범위 내에 실제 피팅된 파라미터 값이 존재하는지 확인한다. 만약 피팅 결과로 얻은 파라미터 값이 시뮬레이션에서 탐색한 범위를 벗어난다면, 이는 모델 피팅 및 비교 과정에서 해석에 문제가 있을 수 있음을 시사한다. 이 경우, 연구자는 파라미터 복원 단계를 다시 수행하여 실제 데이터에서 나타나는 파라미터 범위에 맞게 모델을 수정하거나 실험 설계를 보완해야 한다.

또한, 인간의 행동은 이론적으로 개발된 모델보다 훨씬 복잡하기 때문에, 실제 데이터 분석 과정에서 모델이 모든 행동 패턴을 완벽하게 설명하지 못할 가능성이 크다. 이럴 경우, 연구자는 기존 모델을 보완하기 위해 ‘중요하지 않은(unimportant) 파라미터’들도 함께 고려할 필요가 있다. 예를 들어, 결정 과제에서 좌우 선택에 대한 선호와 같은 기저 편향(bias)을 모델에 포함시키면, 이 편향을 노이즈로 처리하지 않고 별도로 설명할 수 있어, 결과적으로 학습률이나 소프트맥스 파라미터와 같은 중요한 파라미터를 더 정확하게 추정할 수 있다.

Validate (at least) the winning model

앞선 단계에서는 상대적 모델 적합도(relative goodness of fit) 를 평가하여 여러 모델 중에서 가장 적절한 모델을 선택했다. 하지만, 이 모델이 정말로 인간 행동을 유용하게 설명하는지, 즉 “절대적 적합도(absolute goodness of fit)”를 검증하는 과정이 필요하다. 단순히 BIC 값이 낮다고 해서, 혹은 다른 모델보다 더 좋은 성능을 보였다고 해서 반드시 올바른 모델이라고 할 수 없다. 모델 비교(Model Comparison) 과정에서는 단순히 어떤 모델이 다른 모델보다 데이터를 더 잘 설명하는가를 평가한다. 하지만 이것만으로 모델이 실제 행동을 잘 반영하는지 보장할 수 없다.

예를 들어, 모델 A가 모델 B보다 BIC 값이 낮아 더 적합하다고 판단되었지만, 모델 A는 사실 피험자의 행동을 올바르게 재현하지 못할 수도 있다. 반면 모델 B는 BIC 점수는 낮지만, 행동 패턴을 더 정확히 설명할 수도 있다. 즉, 모델 검증이 없다면, 모델이 단순히 수학적으로 좋은 적합도를 보이더라도, 실제로 중요한 행동 패턴을 포착하지 못할 가능성이 크다.

모델 검증 방법

평균 로그-우도(Log-Likelihood per Trial)

모델이 주어진 데이터를 얼마나 잘 설명하는지를 평가하기 위한 절대적 기준(absolute measure) 중 하나이다. 평균 로그-우도(Log-Likelihood per Trial)에서는 각 시행(trial)에서 모델이 실제 선택을 얼마나 정확하게 예측했는지의 확률을 계산하여 평균값을 구한다. \(T\)는 전체 시행(trial) 수, \(c_t\)는 \(t\) 번째 시행에서 실제로 선택된 행동, \(d_{1:t-1}\)는 \(t\) 번째 시행 이전까지의 데이터, \(s_t\)는 \(t\) 번째 시행에서의 상태(state)를 의미한다.

\[\frac{1}{T} \sum_{t=1}^{T} \log p(c_t \mid d_{1:t-1}, s_t, m, \theta)\]

다만 인간의 선택은 종종 확률적으로(stochastic) 이루어지므로, 완벽한 예측을 기대하는 것은 현실적이지 않으며, 최대 가능 로그 우도 값이 얼마인지 알기 어려운 경우가 많다. 또한 환경이 복잡해질수록, 모델이 최적의 선택을 예측하는 것이 어려워지는데 로그 우도 값만으로 모델을 절대적 기준으로 평가하는 것은 한계가 존재한다.

피팅된 파라미터로 모델을 시뮬레이션하여 검증

가장 강력한 모델 검증 방법 중 하나는 “후행 예측 검증(posterior predictive check)”으로, 모델을 시뮬레이션(simulation)하여 실제 데이터와 비교하는 것이다. 예를 들어 앞서 모델을 피팅(fitting)하여 최적의 파라미터(예: \(\alpha\), \(\beta\) 등)를 추정했다면, 이 피팅된 모델을 사용하여 가상의 피험자(virtual participant)들이 수행하는 행동을 시뮬레이션하며 모델이 예측하는 행동 데이터를 생성해야 한다.

이후 모델이 생성한 시뮬레이션 데이터를 실제 데이터와 동일한 방식으로 분석하면서 시뮬레이션된 데이터에서 예상되는 행동 패턴이 실제 데이터에서 관찰된 행동 패턴과 일치하는지 확인해야 한다. 이 때 ‘시뮬레이션 결과가 실제 데이터의 중요한 특성을 반영하는가?’라는 질문에 대답하기 위해 두 가지 검증 방식을 사용할 수 있는데, 정성적 검증(예시: 보상을 많이 받은 조건에서 선택 확률이 증가했다면, 시뮬레이션에서도 같은 경향이 보여야 한다.)과 정량적 검증(예시: 예를 들어, 학습 곡선(learning curve)이 특정한 값(예: \(0.7\))에 수렴했다면, 모델 시뮬레이션에서도 유사한 값에 수렴해야 한다.)을 모두 시도해 볼 수 있다.

일부 연구자들은 시뮬레이션된 데이터가 아니라, 피험자가 실제로 수행한 행동 데이터를 기반으로 후행 예측을 수행하기도 한다. 이 방법에서는 주어진 과거 데이터 \(d_{1:t-1}\) 에 대해, 모델이 현재 시행 \(t\) 에서의 선택 \(c_t\) 를 얼마나 정확히 예측하는지를 평가한다.

\[p(c_t \mid d_{1:t-1}, s_t, m, \theta)\]

\(c_t\)는 \(t\) 번째 시행에서 실제로 선택된 행동, \(d_{1:t-1}\)는 \(t\) 번째 시행 이전까지의 데이터, \(s_t\)는 \(t\) 번째 시행에서의 상태(state), \(m\)은 모델, \(\theta\)는 모델 파라미터를 의미한다. 이 방법은 시뮬레이션 방법과 비슷한 결과를 보일 수도 있지만, 완전히 다른 결과를 초래할 수도 있다. 피험자가 행동을 결정하는 방식과 모델이 행동을 결정하는 방식이 유사하다면, 두 방법(시뮬레이션 vs. 후행 예측)의 결과가 거의 일치할 것이지만 만약 모델이 선택할 가능성이 높은 행동 경로와, 피험자가 실제로 선택한 행동 경로가 매우 다르다면, 후행 예측 결과가 시뮬레이션과 크게 다를 수 있다.

Palminteri et al. (2017)

이 연구에서는 반전 학습(reversal learning) 과제에서 강화 학습 기반 데이터를 서로 다른 학습 전략을 가정하는 두 개의 모델에 피팅한 후, 모델 비교를 수행했다.

모델 A는 단순한 선택 반복 모델 (Choice Kernel Model)으로, 과거의 선택을 반복하는 경향이 있다는 것을 가정하는 모델이다. “이전에 했던 선택을 다시 할 가능성이 높다” 라는 단순한 규칙을 따르지만, 보상 정보는 전혀 고려하지 않는다. 이를 수식적으로 표현하면, 다음과 같다.

\[p(c_t = k) = \frac{\exp(\beta \cdot CK_k)}{\sum_{i} \exp(\beta \cdot CK_i)}\]

모델 B는 Win-Stay Lose-Shift (WSLS) 모델으로, 이전 시행(trial)의 보상 결과에 따라 선택을 바꾸는 전략을 따른다. “보상을 받으면 같은 선택을 유지(Win-Stay), 보상을 받지 못하면 선택을 바꾸는 방식으로, (Lose-Shift)” 이를 수식적으로 표현하면 다음과 같다.

\[p(c_t = k) = \begin{cases} 1 - \epsilon & \text{if } c_{t-1} = k \text{ and } r_{t-1} = 1 \\ \epsilon & \text{otherwise} \end{cases}\]

모델 비교를 수행한 결과, 모델 A(선택 반복 모델)가 모델 B(WSLS 모델)보다 더 높은 적합도(BIC(A) < BIC(B))를 보였고 모델 A가 상대적으로 데이터를 더 잘 설명한다고 평가되었다. 하지만, 여기서 매우 중요한 문제가 발생했다.

모델 A는 과거 선택을 단순히 반복하는 경향을 가정하지만, 반전 학습 과제에서는 보상에 따라 선택을 수정하는 것이 핵심적인 행동 패턴이다! 즉, 모델 A는 “반전 학습”이라는 실험의 본질을 완전히 놓치고 있다. 실험 데이터에서는 보상 확률이 바뀌면 피험자들이 선택을 변경하는 패턴이 관찰되었지만 모델 A를 사용해 데이터를 생성해보니, 피험자들이 보상을 고려하지 않고 무조건 과거 선택을 반복하는 문제가 발생하였다. 그러나 모델 B(WSLS 모델)는 보상을 받지 못하면 선택을 바꾸는 전략을 따르기 때문에, 반전 학습을 일부 재현할 수 있었다. 그러나 모델 A보다 분산을 덜 잡아낸다는 사실이 변하는 것은 아니라서 모델 B가 핵심적인 파라미터를 놓치고 있다는 사실을 인지해야 한다.

Analyze the winning model

모델 기반 분석(model-based analysis)은 최적 모델(winning model)이 검증된 후에 수행해야 한다. 이는 p-hacking(유의성 조작)을 방지하기 위한 중요한 절차로, 연구자가 모델이 행동을 충분히 설명한다고 확신한 후에만 모델 의존적인 분석을 진행해야 한다. 이 단계에서는 특히 모델에서 추출한 잠재 변수(latent variables) 를 활용하여 행동과 신경 메커니즘을 연구하는 것이 핵심이다. 잠재 변수란 관찰된 행동 데이터만으로는 직접 측정할 수 없는, 행동을 생성하는 인지적·신경적 과정의 내부 변수(hidden components)를 의미한다. 예를 들어, 강화 학습 모델에서는 예측 오차(prediction error), 신경경제학 모델에서는 주관적 가치(subjective value), 의사결정 모델에서는 불확실성(uncertainty) 등이 중요한 잠재 변수로 간주될 수 있다.

잠재 변수 분석은 모델을 시뮬레이션하여 변수들이 시간에 따라 어떻게 변화하는지를 추적하는 방식으로 수행된다. 이때 각 참가자의 피팅된 모델 파라미터를 사용하여 개별적인 시뮬레이션을 진행해야 한다. 특히, 참가자가 실험에서 수행한 선택(choice)은 이후 받을 보상에 영향을 미치므로, 잠재 변수의 변화는 참가자가 실제 경험한 선택 결과에 기반해야 한다.

잠재 변수를 추출한 후에는 기존의 관찰 가능한 변수처럼 분석할 수 있다. 첫 번째 방법으로, 행동 데이터와 잠재 변수를 비교하여 특정 행동 패턴이 잠재 변수의 변화와 연관이 있는지 평가할 수 있다. 예를 들어, 예측 오차 \(\delta_t\) 가 클 때 참가자가 선택을 더 자주 변경하는지 분석할 수 있다. 두 번째 방법으로, 신경생리학적 데이터와 잠재 변수를 비교하여 특정 뇌 활동이 특정 잠재 변수와 관련이 있는지를 분석할 수 있다. 예를 들어, 예측 오차 \(\delta_t\) 가 증가할 때 중뇌 도파민 시스템(midbrain dopamine system)이 활성화되는지 평가할 수 있다.(Nassar et al. (2012), Daw et al. (2011), Collins and Frank (2018))

또한, 모델을 사용하면 개인 간 차이를 분석하는 것도 가능하다. 예를 들어, 모델의 피팅된 파라미터(예: 학습률 \(\alpha\), 선택 결정성 \(\beta\))를 나이, 인지 능력, 정신 질환 척도 등과 상관 분석할 수 있다.

Reporting model-based analyses

이 부분은 모델링 연구에서 논문을 작성할 때 연구자가 모델을 개발, 시뮬레이션, 피팅, 비교, 검증한 후, 어떤 결과를 논문에 포함해야 하며, 어떻게 보고해야 하는지를 정리하는 가이드라인을 제시한다. 특히, 모델 선택(model selection), 모델 비교(model comparison), 파라미터 피팅(parameter fitting), 데이터 및 코드 공유(data & code sharing) 와 같은 핵심 요소를 강조하고 있다.

모델 선택(Model Selection)

논문에서 가장 중요한 메시지 중 하나는 “우리 모델이 다른 모델들보다 데이터를 더 잘 설명한다.” 라는 점을 설득력 있게 보여주는 것이다. 이를 위해, 모델 복원 분석(model recovery analysis)과 모델 비교 결과를 투명하게 보고해야 한다.

1. 모델 복원 분석 (Model Recovery Analysis) 모델 비교 결과를 신뢰할 수 있으려면, 시뮬레이션 데이터에서 모델을 올바르게 구분할 수 있어야 한다. 즉, 이상적인 조건에서 실험 및 분석 방법이 서로 다른 모델을 얼마나 잘 구별할 수 있는지 평가해야 한다. 이를 가장 효과적으로 시각화하는 방법은 혼동 행렬(confusion matrix) 를 사용하는 것이다.

혼동 행렬(confusion matrix) 는 특정 모델이 생성한 데이터를, 모델 비교 알고리즘이 올바르게 식별하는지를 보여준다. 만약 모델 비교 결과가 논문의 핵심이라면, 혼동 행렬을 본문(main text)에서 제시하는 것이 좋다. 모델 비교가 논문의 부차적인 요소라면, 부록(supplementary materials)에 포함해도 된다.

1. 각 모델이 최적 피팅된 참가자 수 (Number of Subjects Best Fit by Each Model)

모델 비교의 직관적인 시각화 방법 중 하나는 각 모델이 몇 명의 참가자에게 최적 피팅되었는지 히스토그램으로 보여주는 것이다. 만약 모든 참가자가 동일한 모델에 의해 가장 잘 피팅된다면, 연구 결론이 명확해진다. 하지만 일부 참가자가 다른 모델에 의해 더 잘 피팅된다면, 이는 사람들이 다른 전략을 사용할 가능성이 있음을 의미한다. 또는, 현재 고려한 모델들 사이에 ‘진짜 정답’이 존재하지 않을 가능성도 있다. 따라서, 다양한 모델이 피팅될 가능성이 있다는 점을 논문에서 솔직하게 인정해야 한다.

1. 초과 확률(Exceedance Probability)

모델 비교 결과를 보다 정량적으로 제시하려면, 특정 모델이 전체 데이터를 가장 잘 설명할 확률을 계산할 수 있다. Rigoux et al. (2014)의 방법을 사용하면, 초과 확률(Exceedance Probability) 을 계산할 수 있다. 이러한 확률은 히스토그램이나 표(table) 형태로 보고할 수 있다.

또한 모델을 보고할 때, 모델이 기존의 질적(qualitative) 패턴을 설명할 수 있는지를 반드시 포함해야 한다. 단순히 BIC나 우도를 기반으로 모델을 선택하는 것이 아니라, “이 모델이 우리가 관찰한 중요한 행동 패턴을 실제로 재현할 수 있는가?” 를 평가해야 한다. 모델이 인간 행동에서 나타나는 질적 패턴을 설명하지 못한다면, 아무리 높은 적합도를 보여도 그 모델은 좋은 모델이 아니다.

파라미터 피팅(Parameter Fits)

모델 연구에서는 행동 데이터를 바탕으로 최적의 모델 파라미터를 추정하는 과정이 필수적이다. 이 과정에서 연구자는 파라미터 값을 투명하게 보고해야 하며, 단순히 평균과 표준 편차만 제공하는 것은 충분하지 않다.

실험에 참가한 각 참가자의 개별 피팅된 파라미터 값을 시각화하는 것이 중요할 수 있다. 예를 들어, 히스토그램(histogram) 또는 점 클라우드(cloud of points) 그래프 를 통해 각 파라미터가 얼마나 다양한지를 직관적으로 보여줄 수 있다. 만약 특정 파라미터가 상한 또는 하한에 많이 몰려 있다면, 이는 모델에 문제가 있을 가능성을 시사한다. 각 모델 파라미터 간의 관계를 이해하려면, 파라미터 간 상관 관계를 시각화하기 위해 산점도(scatter plot)를 활용하는 것이 좋다.

또한 모든 파라미터 피팅 과정은 철저한 파라미터 복원 분석을 기반으로 해야 한다. 만약 시뮬레이션 데이터에서 파라미터를 제대로 복원할 수 없다면, 실제 데이터에서도 신뢰할 수 없는 결과가 나올 가능성이 높다.

데이터 및 코드 공유 (Share Your Data and Code)

모델링 연구의 투명성을 높이기 위해, 연구자가 원시(raw) 데이터와 분석 코드까지 공개하는 것 공유하는 것이 바람직하다. 데이터 및 코드는 GitHub, DataVerse 같은 공공 저장소를 이용해 공개할 수 있다. 하지만 데이터가 협력 연구자의 소유이거나 추가 분석이 계획된 경우, 공유가 어려울 수도 있다. 이럴 때는, 요청이 있을 경우 연구자가 데이터를 제공할 수 있도록 정리해 두는 것이 좋다.

모든 모델링 결과를 보고해야 하는가?

일부 연구자는 이미 확립된 모델(예: 기존 연구에서 사용된 모델)을 적용하는 경우, 일부 분석을 생략하고 가장 흥미로운 결과만 보고하고 싶어할 수 있다. 그러나 특정 모델이 다른 연구에서는 잘 작동했더라도, 새로운 데이터나 실험 환경에서는 다르게 작동할 수 있는 점, 많은 기존 모델들이 체계적으로 검증되지 않았을 가능성이 있다는 점, 연구자가 사용한 모델링 방법이 올바르게 적용되었음을 보여줘야 한다는 점 등의 이유 때문에 모델 비교, 파라미터 피팅, 모델 검증 등의 결과를 투명하게 보고하는 것이 필수적이다.

What now?

Looping Back: 모델을 개선하는 반복 과정

모델링 연구는 한 번의 분석으로 끝나는 것이 아니라, 지속적인 개선과 반복적인 수정(looping back)이 필수적이다. George Box(1979)의 “모든 모델은 틀렸다. 그러나 어떤 모델은 유용하다.” 의 유명한 말처럼, 완벽한 모델은 존재하지 않으며, 모델을 보다 유용하게 만들기 위해 다음과 같은 단계를 고려해야 한다.

1. 모델을 개선하여 데이터와의 차이를 줄이기 모델이 실제 데이터와 완벽하게 일치하는 경우는 거의 없다. 따라서, 모델이 설명하지 못하는 행동 패턴을 분석하고, 이를 보완할 방법을 모색해야 한다. 또한 참가자가 특정 방향을 더 선호하는 경향이 있거나, 일정 확률로 실수를 하는 경우 이를 모델에 반영하면 더 나은 적합도를 얻을 수 있다.

기존 모델이 데이터의 핵심 패턴을 설명하지 못한다면, 완전히 새로운 가설을 기반으로 한 모델을 설계하는 것이 필요할 수 있다.

• 모델이 데이터를 얼마나 정확히 설명하는가?
• 설명하지 못하는 행동 패턴이 있다면, 어떤 요소가 빠져 있는가?
• 모델이 기존 데이터에서 보이는 불일치를 해결하려면 어떻게 수정해야 하는가?

등의 질문을 생각해 볼 수 있다.

1. 모델의 일반화 가능성 테스트하기 좋은 모델은 특정 실험 데이터에만 맞추는 것이 아니라, 새로운 환경에서도 예측력을 유지해야 한다. 즉, 모델이 일반적인 인간 행동을 반영하는지를 검증해야 한다. 빠르게 적용할 수 있는 방법은 동일한 모델을 사용하여 새로운 조건에서 실험을 진행하고, 모델이 동일한 방식으로 행동을 설명하는지 확인하는 것이다.

만약 새로운 데이터를 수집하기 어려운 경우, 다른 연구자가 공유한 데이터를 이용하여 모델을 검증할 수도 있다. 또한 특정한 실험 조건에서만 잘 작동하는 모델이라면, 일반화 가능성이 낮을 수 있다.

• 모델이 실험 환경에만 특화된 것이 아니라, 일반적인 행동 패턴을 반영하는가?
• 다른 실험에서도 모델이 일관된 예측을 제공하는가?
• 모델이 특정 데이터셋에서만 높은 적합도를 보이는 것은 아닌가?

등의 질문을 생각해 볼 수 있다.

Using Advanced Techniques: 더 발전된 모델링 기법 활용하기

기본적인 모델링 기법인 최대우도추정(MLE)과 BIC 기반 모델 비교는 비교적 단순하고 접근성이 높지만, 한계가 존재한다. 아래에서는 대표적인 모델링 기법을 소개한다.

MAP

첫 번째로, 최대 사후 확률(MAP, Maximum A Posteriori) 추정 방법이 있다. MLE는 데이터를 기반으로 최적의 파라미터를 추정하지만, 사전 정보(prior)를 고려하지 않는다. MAP 추정을 활용할 때 고려해야 할 주요 질문은 사전 정보를 추가하면 파라미터 추정이 얼마나 개선되는가, 사전 정보의 신뢰성을 어떻게 평가할 것인가, 그리고 사전 정보가 잘못 설정되었을 때 모델 결과에 미치는 영향을 어떻게 분석할 것인가이다. MAP 추정에 대한 자세한 내용은 Gershman(2016), Daw(2011), Katahira(2016)의 연구를 참고할 수 있다.

MCMC

두 번째로, 마르코프 체인 몬테카를로(MCMC)를 이용한 사후 확률 분포 추정 방법이 있다. MLE와 MAP은 특정한 값만을 제공하는 점 추정(point estimate) 방식이므로, 파라미터의 불확실성을 반영하기 어려운 반면 MCMC는 사후 확률 분포(posterior distribution)를 샘플링하여 파라미터의 신뢰 구간(uncertainty)을 추정하는 데 유용한 방법이다. 연구자는 MCMC 샘플링이 기존 점 추정 방식보다 더 많은 정보를 제공하는지, 파라미터의 불확실성을 충분히 반영할 수 있는지, 계층적 분석이 연구 질문에 적절한지를 고려해야 한다. 이에 대한 자세한 연구는 Lee(2011), Lee & Wagenmakers(2014), Wiecki et al.(2013)에서 확인할 수 있다.

ABC

세 번째로, 일부 모델에서는 우도를 직접 계산하는 것이 현실적으로 매우 어렵거나 불가능할 수 있다. 예를 들어, 연속적인 움직임(continuous movement)을 모델링하거나, 관측되지 않은 선택이 포함된 경우 계산이 복잡해진다. 이러한 경우, Approximate Bayesian Computation(ABC) 방법을 활용하면 우도를 직접 계산하는 대신 시뮬레이션을 통해 근사적인 결과를 얻을 수 있다. 연구자는 기존 방법으로 우도를 계산하는 것이 비효율적인지, 근사 기법을 사용하더라도 모델이 정확하게 작동하는지, 그리고 최적화 알고리즘을 변경했을 때 결과가 얼마나 안정적인지를 평가해야 한다. 이에 대한 자세한 연구는 Turner & Sederberg(2012), Sunnåker et al.(2013), Acerbi & Ji(2017), Acerbi(2018)에서 찾아볼 수 있다.

Baysian model selection

마지막으로, 베이지안 모델 선택(Bayesian Model Selection) 기법을 활용할 수 있다. 연구자는 단순한 BIC 기반 모델 비교보다 베이지안 모델 선택이 더 적절한지, 그리고 집단 수준에서 모델 선택을 수행할 필요가 있는지를 신중하게 고려해야 한다. 이에 대한 보다 자세한 논의는 Rigoux et al.(2014), Piray et al.(2018)에서 확인할 수 있다.