Ten simple rules for the computational modeling of behavioral data - Example bandit task

An illustrative example: the multi-armed bandit task

논문에서 제시하는 10가지 모델링 규칙은 매우 일반적이지만, 이를 보다 구체적으로 설명하기 위해 강화학습(reinforcement learning) 모델을 활용한 선택 과제(choice task) 를 예시로 들고 있다. 이 논문에서 다루는 예제들은 사람들이 어떻게 보상을 극대화하는지를 학습하는 과정을 분석하는 것이 목표이다. 특히, 최적의 선택이 처음에는 알려져 있지 않은 상황에서 학습이 어떻게 진행되는지를 연구한다.

멀티 암드 밴딧(Multi-Armed Bandit) 과제란?

이 실험은 여러 개의 슬롯머신(slot machine, 또는 “one-armed bandit”) 중 하나를 선택하는 방식으로 진행된다. 실험 참가자는 T번의 선택(trials) 을 수행하며, K개의 슬롯머신 중 하나를 선택해야 한다. 각 슬롯머신 \(k\) 는 선택(trial \(t\))될 때, 특정한 확률 \(θ_k\) 로 보상(reward, \(r_t\))을 지급한다.

즉, 슬롯머신 \(k\) 를 선택했을 때, 보상 \(r_t\) 을 받을 확률은 \(θ_k\) 이며, \(θ_k\) 는 슬롯머신마다 다르며, 실험 참가자는 이를 사전에 알지 못한다(unknown to the subject). 가장 단순한 실험에서는 보상 확률 \(θ_k\) 가 시간에 따라 변하지 않고 고정(fixed)되어 있다.

멀티 암드 밴딧 과제의 실험 변수

이 실험에서는 다음과 같은 3가지 주요 변수를 설정할 수 있다.

• 시행 횟수 (\(T\)): 참가자가 선택을 몇 번 반복하는가?
• 슬롯머신 개수 (\(K\)): 몇 개의 슬롯머신이 있는가?
• 보상 확률 (\(θ_k\)): 각 슬롯머신이 보상을 줄 확률이 얼마인가?

이러한 변수 설정이 실험의 결과에 중요한 영향을 미치며, 논문에서 사용한 기본 실험 설정은 다음과 같다.

• 시행 횟수: \(T = 1000\)
• 슬롯머신 개수: \(K = 2\)
• 슬롯머신의 보상 확률:
• 슬롯머신 1: \(θ_1 = 0.2\) (20% 확률로 보상)
• 슬롯머신 2: \(θ_2 = 0.8\) (80% 확률로 보상)

즉, 한 참가자는 두 개의 슬롯머신 중 하나를 선택해야 하며, 각각의 슬롯머신이 보상을 줄 확률은 미리 정해져 있지만 참가자는 이를 모른다. 실험 참가자는 반복적인 선택을 통해 어느 슬롯머신이 더 높은 보상을 주는지 학습해야 한다.

이 과제가 왜 중요한가?

멀티 암드 밴딧 과제는 탐색-활용(exploration-exploitation) 문제를 연구하는 데 매우 유용하다. 탐색(Exploration)은 더 나은 선택을 하기 위해 미지의 선택지를 시도하는 것이며, 활용(Exploitation)은 현재까지 학습한 정보를 바탕으로 가장 보상이 높을 것으로 예상되는 선택지를 선택하는 것이라 할 수 있다.

예를 들어, 초반에는 두 슬롯머신의 보상 확률을 모른 상태이므로 여러 번 선택을 시도하며 탐색(exploration) 을 수행해야 한다. 실험이 진행됨에 따라 더 높은 확률로 보상을 주는 슬롯머신(슬롯머신 2, \(θ_2\) = 0.8)을 인식하고 이를 점점 더 많이 선택하는 전략(활용, exploitation) 을 사용할 것이다. 이 과제는 강화학습 모델을 테스트하는 데 매우 적합하며, 다양한 학습 알고리즘을 비교하는 데 사용할 수 있다.

Box 1. Example: Modeling behavior in the multi-armed bandit task.

이 논문에서는 Multi-Armed Bandit Task에서 사람들이 어떻게 행동하는지를 설명하는 다섯 가지 모델을 제시하고 있다. 각 모델의 핵심 개념과 수식을 설명하면 다음과 같다.

Model 1: Random Responding (랜덤 응답 모델)

이 모델은 참가자가 과제에 전혀 몰입하지 않고 단순히 무작위로 버튼을 누르는 경우를 가정한다. 그러나 참가자가 특정 선택지에 대한 선호도(bias)를 가질 수도 있다고 본다. 이 선호도는 파라미터 \(b\) 로 표현되며, 다음과 같이 선택 확률을 결정한다.

\[p_1 = b, \quad p_2 = 1 - b\]

즉, \(b\) 값이 0.5이면 두 선택지를 균등한 확률로 선택하고, \(b\) 값이 1에 가까울수록 특정 선택지를 선호하게 된다. 이 모델은 단 하나의 자유 파라미터 \(b\) 만을 가진다

Model 2: Noisy Win-Stay-Lose-Shift (노이즈가 추가된 승리-유지, 패배-전환 모델)

이 모델은 보상을 받으면 같은 선택을 반복하고, 보상을 받지 못하면 선택을 바꾸는 단순한 전략을 따른다. 그러나 이 전략을 항상 적용하는 것이 아니라 확률적으로 적용하는데, 확률 \(1 - \epsilon\) 로 win-stay-lose-shift 규칙을 따르고, 확률 \(\epsilon\) 로 랜덤 선택을 한다. 이 모델에서 선택 확률은 다음과 같다.

\[p_k^t = \begin{cases} 1 - \frac{\epsilon}{2}, & \text{if } (c_{t-1} = k \text{ and } r_{t-1} = 1) \text{ OR } (c_{t-1} \neq k \text{ and } r_{t-1} = 0) \\ \frac{\epsilon}{2}, & \text{if } (c_{t-1} \neq k \text{ and } r_{t-1} = 1) \text{ OR } (c_{t-1} = k \text{ and } r_{t-1} = 0) \end{cases}\]

이 모델은 전체적인 랜덤성 수준을 조절하는 단 하나의 자유 파라미터 \(\epsilon\) 을 가진다.

Model 3: Rescorla-Wagner (레스콜라-와그너 학습 모델)

이 모델은 참가자가 이전 결과를 바탕으로 각 슬롯 머신(옵션)의 기대 가치를 학습한다고 가정한다. 학습 규칙은 Rescorla-Wagner 학습 규칙을 따른다.

\[Q_k(t+1) = Q_k(t) + \alpha (r_t - Q_k(t))\]

여기서,

\(Q_k(t)\) 는 시간 \(t\) 에서의 선택지 \(k\) 의 기대 가치,
\(r_t\) 는 시간 \(t\) 에서 받은 보상,
\(\alpha\) 는 학습률로, 0과 1 사이의 값을 가지며, 보상이 가치 업데이트에 미치는 영향을 조절한다.

의사결정 과정은 Softmax 선택 규칙을 따른다.

\[p_k^t = \frac{\exp(\beta Q_k^t)}{\sum_{i=1}^{K} \exp(\beta Q_i^t)}\]

여기서, \(\beta\) 는 ‘inverse temperature’로, 값이 크면 높은 가치를 가진 옵션을 더 확실하게 선택하고, 값이 작으면 랜덤한 선택을 많이 하게 된다. 이 모델은 두 개의 자유 파라미터 \((\alpha, \beta)\) 를 가진다.

Model 4: Choice Kernel (선택 경향성 모델)

이 모델은 사람들이 단순히 기대 가치를 기반으로 선택하는 것이 아니라, 과거에 선택했던 행동을 반복하는 경향이 있음을 반영한다. 이를 위해 Choice Kernel이라는 개념을 도입한다. Choice Kernel은 최근 선택했던 행동의 빈도를 추적하며, 다음과 같은 업데이트 방식을 따른다.

\[CK_k(t+1) = CK_k(t) + \alpha_c (a_k(t) - CK_k(t))\]

여기서, \(a_k(t) = 1\) 이면 선택한 옵션이고, 그렇지 않으면 0이다. \(\alpha_c\) 는 선택 경향성을 업데이트하는 학습률이다. 이후 선택 확률은 Softmax 형태로 결정된다.

\[p_k = \frac{\exp(\beta_c CK_k)}{\sum_{i=1}^{K} \exp(\beta_c CK_i)}\]

이 모델은 두 개의 자유 파라미터 \((\alpha_c, \beta_c)\) 를 가진다.

Model 5: Rescorla-Wagner + Choice Kernel (강화 학습 + 선택 경향성)

이 모델은 강화 학습 모델과 선택 경향성 모델을 결합한 가장 복잡한 모델이다. 이 모델에서는 기대 가치를 업데이트하는 Rescorla-Wagner 모델과 과거 선택 경향성을 반영하는 Choice Kernel 모델이 함께 사용된다.

최종적으로 선택 확률은 다음과 같이 계산된다.

\[p_k = \frac{\exp(\beta Q_k + \beta_c CK_k)}{\sum_{i=1}^{K} \exp(\beta Q_i + \beta_c CK_i)}\]

즉, 선택 확률이 기대 가치 \(Q_k\) 와 선택 경향성 \(CK_k\) 의 합에 기반하여 결정된다. 이 모델은 총 네 개의 자유 파라미터 \((\alpha, \beta, \alpha_c, \beta_c)\) 를 가진다.

이 다섯 개 모델은 참가자가 Multi-Armed Bandit Task에서 어떻게 선택을 하는지를 수학적으로 설명하기 위한 것이다. 모델의 복잡도는 점점 증가하며, 가장 간단한 모델은 Random Responding이고, 가장 복잡한 모델은 Rescorla-Wagner + Choice Kernel 모델이다.

• Random Responding: 무작위 선택 (자유 파라미터: \(b\))
• Noisy Win-Stay-Lose-Shift: 보상에 따라 반복 또는 변경 (자유 파라미터: \(\epsilon\))
• Rescorla-Wagner: 강화 학습 (자유 파라미터: \(\alpha, \beta\))
• Choice Kernel: 과거 선택 반복 경향 반영 (자유 파라미터: \(\alpha_c, \beta_c\))
• Rescorla-Wagner + Choice Kernel: 강화 학습 + 선택 경향 (자유 파라미터: \(\alpha, \beta, \alpha_c, \beta_c\))

각 모델은 인간의 학습 및 의사결정 과정을 수량화할 수 있도록 하며, 연구자들은 실험 데이터를 이 모델에 적합시켜 인간 행동의 기저 메커니즘을 분석할 수 있다.

Box 2. Example: simulating behavior in the bandit task.

1. 행동 시뮬레이션을 위한 실험 설정

행동을 시뮬레이션하기 위해 먼저 실험 조건을 정의해야 한다. 여기서 시뮬레이션의 실험 조건은 실제 실험과 동일해야 한다. 실험과 다른 설정을 사용하면 결과를 직접 비교하기 어려워진다.

• 총 시행 횟수 \(T = 1000\)
• 선택지(슬롯 머신)의 개수 \(K = 2\)
• 각 슬롯 머신의 보상 확률:
• Bandit 1: \(p = 0.2\)
• Bandit 2: \(p = 0.8\)

2. 모델 파라미터 설정

각 모델의 자유 파라미터를 정의해야 하며, 이를 설정하는 방법 중 하나는 사전 확률 분포(prior distribution)에서 무작위로 샘플링하는 것이다. 사전 분포(prior distribution)은 가능한 한 넓게(broad) 설정하는 것이 일반적이나, 특정 모델에 대한 기존 연구 결과가 있다면, 문헌에서 보고된 값을 참고하여 설정할 수도 있다.

3. 시뮬레이션 과정

시뮬레이션은 다음과 같은 절차를 따른다.

1. 모델에 따라 각 선택지의 선택 확률 \(p_k(1)\) 을 계산한 후, 그 확률에 따라 선택 \(a_1\) 를 결정한다.
2. 선택한 슬롯 머신의 보상 확률을 고려하여 \(r_1\) (보상 여부)를 결정한다.
3. Model 2~5는 이전 선택(action) 및 보상(outcome) 정보를 이용하여 다음 시행의 선택 확률을 업데이트한다. 즉, \(p_k(t)\) 를 갱신하여 \(a_t\) 의 확률을 조정한다.
4. 이 과정을 \(T\) 번 반복하여 시뮬레이션을 완료한다. 이를 통해 한 명의 가상 참가자(simulated participant)의 데이터를 생성할 수 있다.
5. 단일 시뮬레이션만으로는 모델의 특성을 충분히 이해하기 어렵기 때무에, 여러 파라미터 값에 대해 반복적인 시뮬레이션을 수행하여 모델이 어떻게 동작하는지 확인한다.

4. 시뮬레이션 결과 분석

모델의 행동을 이해하기 위해 모델 독립적인 측정값(model-independent measures)을 정의하고 이를 시각화한다.

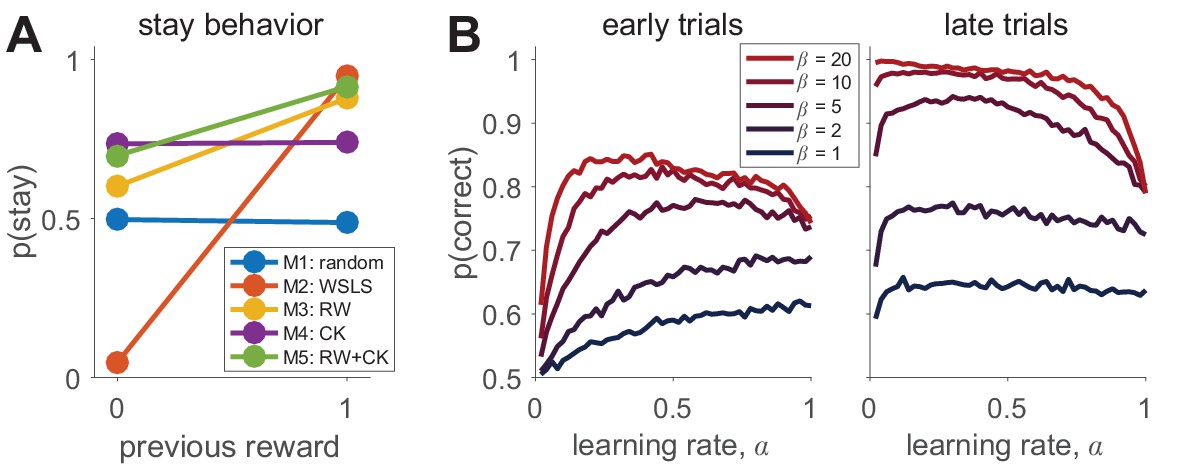
이 예시에서 알아볼 측정값은 \(p(stay)\) (이전 시행에서 같은 선택을 유지할 확률)이다. “나는 피드백에 따라 행동을 바꿀 것인가?” 라는 질문에 대한 대답으로, 특정 모델이 보상에 어떻게 반응하는지를 보여준다. Win-Stay-Lose-Shift(WSLS) 모델(Model 2)에서는 보상에 강하게 의존하지만, Random Responding(Model 1)에서는 보상과 무관하였으며, 이는 Box 2—figure 1A에서 확인 가능하다.

두 번째 측정값은 \(p(correct)\) (올바른 선택을 할 확률)이다. 이는 “나는 학습을 통해 정답을 찾고 있는가?” 라는 질문의 대답이며, 학습이 진행됨에 따라 \(p(correct)\) 가 증가해야 한다. Box 2—figure 1B에서 Model 3(Rescorla-Wagner) 시뮬레이션 결과를 확인할 수 있다.

figure 1. Simulating behavior in the two-armed bandit task.

5. 모델 파라미터에 따른 행동 변화

Box 2—figure 1B에서는 Model 3(Rescorla-Wagner)의 파라미터 값 변화에 따른 학습 성능을 분석한다. 초기 학습(early trials)에서 \(\alpha\) 가 크면 학습 속도가 빠르지만, \(\beta\) 가 클수록 최적의 \(\alpha\) 값은 작아진다. 즉, 높은 \(\beta\) 값(결정적 선택일 때)에서는 낮은 \(\alpha\) 가 학습을 더 잘 유도한다.

후기 학습(late trials)에서는 높은 \(\beta\) 값에서는 \(\alpha\) 가 너무 크면 학습이 불안정해지고, \(p(correct)\) 가 감소한다. 즉, 높은 \(\alpha\) 값이 항상 좋은 것은 아님. 학습이 어느 정도 안정화되면 \(\alpha\) 가 너무 크면 불리할 수도 있다.

특정 \(\beta\) 값에서 \(\alpha\) 가 지나치게 작거나 크면 학습이 비효율적이었으며, 초기에는 높은 \(\alpha\) 가 빠른 학습을 유도하지만, 후기에는 낮은 \(\alpha\) 가 더 안정적인 성능을 보인다.

6. 모델 독립적 측정값을 어떻게 선택할 것인가?

모델 독립적인 측정값을 정하는 것은 쉬운 문제가 아니다.

측정값은 전체적인 행동 특성을 반영해야 하며, 모델 간 차이를 진단할 수 있어야 한다. 실험의 연구 목적에 따라 측정값을 신중히 선택해야 한다. 예를 들어, 특정 연구에서는 보상에 대한 반응성이 중요할 수도 있고, 다른 연구에서는 탐색 vs. 활용 전략(exploration-exploitation tradeoff)이 핵심일 수도 있다.

Box 3. Example: contending with multiple local maxima.

이 부분에서는 Collins & Frank (2012)의 혼합 강화 학습과 작업 기억 모델을 예제로 사용하여 실제 최적화 과정에서 발생할 수 있는 문제를 보여준다. 최적화 알고리즘은 주어진 함수의 최댓값(또는 최솟값)을 찾는 것을 목표로 하지만, 실제로는 전역 최댓값(global maximum)이 아닌 지역 최댓값(local maximum)에 수렴할 수 있다. 즉, 초기값을 어디에서 설정하느냐에 따라 서로 다른 최적해가 나올 수 있으며, 최적화가 반드시 가장 좋은 해(전역 최적해)를 찾는다고 보장할 수는 없다. 특히, 모델의 로그-우도 함수(log-likelihood function)가 여러 개의 지역 최대 값을 가질 경우, 최적화 과정이 특정 지역 최대에서 멈춰버릴 가능성이 높다. 이는 강화 학습 모델과 같은 복잡한 비선형(non-linear) 모델에서 자주 발생하는 문제이다.

Collins & Frank (2012)의 모델은 강화 학습(reinforcement learning)과 작업 기억(working memory)을 혼합한 모델로, 가장 단순한 버전에서는 두 개의 주요 파라미터를 가진다. \(\kappa\): 작업 기억(working memory)의 영향력을 나타내는 파라미터 \(\alpha\): 강화 학습(learning rate, 학습률)을 나타내는 파라미터 2가지이다. 이 모델을 특정 실험과 결합하여 최적화를 수행하면, 로그-우도 함수가 여러 개의 지역 최대 값을 가지는 복잡한 표면(log-likelihood surface)을 형성한다. 즉, 최적화 알고리즘이 어디에서 시작하느냐에 따라 서로 다른 최적해에 수렴할 수 있다. figure 2 (왼쪽 그래프)를 보면, 이 모델의 로그-우도 표면이 여러 개의 지역 최대를 포함하고 있음을 확인할 수 있다.

figure 2. An example with multiple local minima.

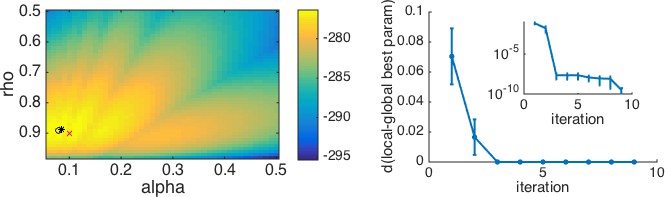
이 그림에서 최적화 방법과 초기값 설정에 따라 서로 다른 최적해가 나올 수 있음을 보여주는 다양한 결과가 존재한다. 빨간 X 표시는 실제 데이터 생성에 사용된 참값(generative parameters), 검은 원(●)은 브루트 포스 탐색(Brute Force Search)로 찾은 최적해, 검은 별(★)은 Matlab의 fmincon 최적화 함수와 여러 개의 초기값을 사용한 최적해를 의미한다. 이 결과는 최적화 방법과 초기값 설정이 매우 중요하며, 하나의 최적해만으로는 모델이 실제 데이터를 얼마나 잘 설명하는지 확신하기 어렵다는 점을 강조한다.

지역 최대 문제를 해결하는 방법: 다중 반복 최적화 (Multiple Iteration Optimization)

지역 최대 문제를 해결하는 가장 효과적인 방법은 최적화 과정을 여러 번 반복하는 것이다. 즉, 다양한 초기값에서 최적화를 수행하고, 가장 높은 로그-우도를 반환하는 파라미터를 선택하는 방식이다.

1. 최적화 절차를 여러 번 실행한다 일반적으로 최적화 알고리즘은 초기값에서 출발하여 최적해를 탐색하기 때문에, 초기값에 따라 서로 다른 최적해를 찾을 수 있다. 이를 방지하기 위해 서로 다른 초기값에서 여러 번 최적화를 실행해야 한다. 예를 들어, 10번, 20번, 혹은 100번 이상의 최적화를 수행하여 로그-우도 값이 어떻게 변화하는지를 살펴볼 수 있다.

2. 각 실행에서 얻은 최적해를 저장한다 각 실행에서 계산된 최적 로그-우도(log-likelihood)와 해당하는 파라미터 값들을 기록하고, 가장 높은 로그-우도를 반환하는 최적해를 선택한다. 이렇게 하면, 지역 최대에서 멈추는 문제를 줄이고 전역 최적해를 찾을 가능성을 높일 수 있다.

3. 로그-우도의 수렴 여부를 확인한다 최적화를 반복 수행할 때, 초기에는 로그-우도 값이 계속 증가하지만, 어느 순간부터 더 이상 개선되지 않고 일정한 값에 수렴하는 경향을 보인다. 즉, 로그-우도가 충분히 큰 값에 도달한 후 더 이상 증가하지 않는다면, 우리는 전역 최적해에 가까워졌다고 판단할 수 있다.

최적화 결과를 시각적으로 평가하는 방법

figure 2 (오른쪽 그래프)에서는 최적화 결과를 분석하는 방법을 보여준다. X축은 초기값 개수 (\(n\), 즉 최적화를 반복 수행한 횟수), Y축은 \(n\) 번째 최적화 실행에서 얻은 파라미터 값과 최종 최적 파라미터 값 사이의 거리이다. 이 그래프를 보면, 반복 횟수가 증가할수록 최적 로그-우도와 최적 파라미터 값이 수렴하는 모습을 확인할 수 있다. 즉, 충분한 반복을 수행하면 전역 최적해에 가까운 값을 얻을 수 있으며, 몇 번의 실행이 필요한지 경험적으로 결정할 수 있다.

특히, 작은 그래프(inset graph)에서 로그 스케일로 나타낸 결과를 보면, 세 번째 반복 이후에는 추가적인 개선이 거의 없음을 확인할 수 있다. 이는 최적화를 무한정 반복할 필요 없이, 일정 횟수 이상 반복하면 전역 최적해를 충분히 근사할 수 있음을 의미한다.

Box 4. Example: parameter recovery in the reinforcement learning model.

이 부분에서는 Rescorla-Wagner 모델(Model 3)의 파라미터 복원(Parameter Recovery) 실험을 수행한 예제를 설명하고 있다. 즉, 실제 실험 데이터를 분석하기 전에, 모델이 제대로 작동하는지 검증하는 과정을 보여준다.

1. Recap: 실험 설정

이 실험에서는 이전과 동일한 두-팔 도박 과제(two-armed bandit task)를 사용하여 파라미터 복원 실험을 수행하였다. 슬롯 머신의 평균 보상값 설정은 다음과 같았다: Bandit 1: \(p = 0.2\), Bandit 2: \(p = 0.8\)

\(T = 1000\) 번 시행하였으며, Rescorla-Wagner 모델을 사용하여 행동을 시뮬레이션하였다. 해당 모델의 학습률(\(\alpha\))과 소프트맥스 파라미터(\(\beta\))는 다음과 같은 분포에서 샘플링되었다.

\[\alpha \sim U(0, 1), \quad \beta \sim \text{Exp}(10)\]

\(\alpha\) (학습률)는 0에서 1 사이의 균등 분포(Uniform Distribution) 에서 샘플링되었으며, \(\beta\) (소프트맥스 선택성)는 평균이 10인 지수 분포(Exponential Distribution) 에서 샘플링되었다. 이렇게 설정된 \(\alpha\) 와 \(\beta\) 값을 이용하여 Rescorla-Wagner 모델을 사용해 가짜 데이터를 생성하고, 이후 최대 우도 추정(MLE) 방법을 이용해 파라미터를 복원하였다. 이 과정을 총 1000번 반복하여, 매번 새로운 \(\alpha\) 와 \(\beta\) 값을 샘플링하고 이를 복원하는 실험을 수행하였다.

2. 결과 분석

figure 3에서는 시뮬레이션한 파라미터 값과 복원된 파라미터 값의 관계를 시각적으로 표현하였다. 전반적으로, 시뮬레이션된 값과 복원된 값이 잘 일치하는 것을 확인할 수 있다. 이는 모델이 설정된 값을 비교적 정확하게 복원할 수 있으며, 신뢰할 수 있는 방식으로 데이터를 설명할 수 있음을 시사한다.

figure 3. Parameter recovery for the Rescorla Wagner model (model 3) in the bandit task with 1000 trials.

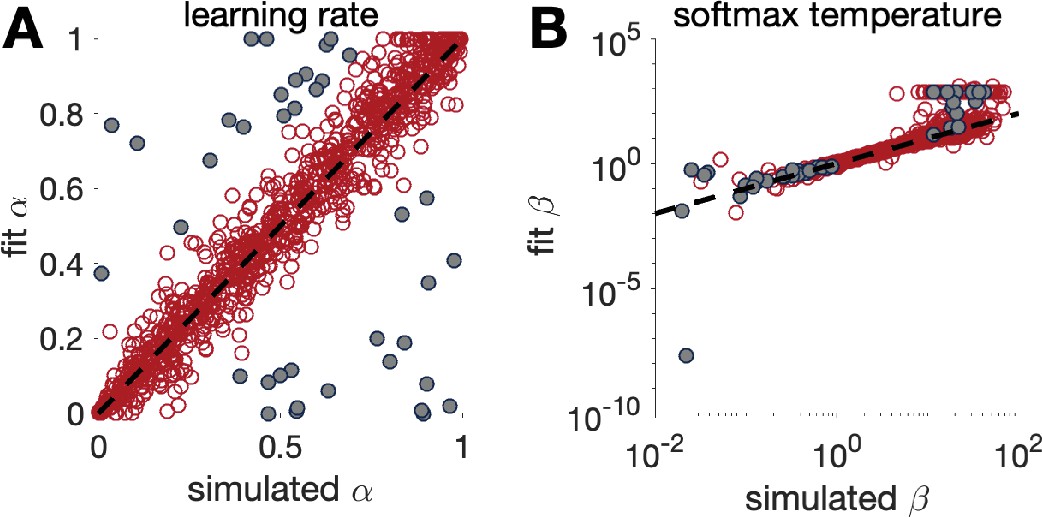
소프트맥스 파라미터 \(\beta\)의 경우, \(1 < \beta < 10\) 범위에서는 매우 정확하게 복원되나 \(\beta\) 값이 1보다 작거나 10보다 크면 복원 성능이 떨어졌다. 즉, 극단적으로 낮거나 높은 \(\beta\) 값에서는 모델이 올바르게 파라미터를 복원하지 못할 가능성이 높다고 할 수 있다. 학습률 \(\alpha\) 의 복원 성능의 경워, 특정 상황에서 학습률 \(\alpha\) 의 복원 성능이 낮아지는 경우가 관찰되었는데, 복원된 \(\alpha\) 값과 실제 시뮬레이션된 값 사이의 오차 \(\vert \alpha_{\text{sim}} - \alpha_{\text{fit}} \vert > 0.25\) 가 되는 경우를 회색 점(grey dots)으로 표시하였다.

이러한 회색 점을 분석해보면, \(\beta\) 값이 특정 범위(1~10)를 벗어날 때 \(\alpha\) 의 복원 성능이 나빠지는 경향이 관찰되었다. 즉, \(\beta\) 값이 너무 크거나 너무 작을 경우, 학습률 \(\alpha\) 를 신뢰할 수 있는 방식으로 추정하는 것이 어려울 수 있다.

Box 5. Example: confusion matrices in the bandit task.

1. 모델 복원 실험 개요

두 개의 슬롯 머신(Bandit)의 평균 보상값과 수행 시간 설정은 이전 예제와 동일하다.

• Bandit 1: \(p = 0.2\)
• Bandit 2: \(p = 0.8\)
• \(T = 1000\) 번

각 모델의 파라미터 값은 특정 분포에서 샘플링하여 설정되었다.

• Model 1: \(b \sim U(0,1)\)
• Model 2: \(\epsilon \sim U(0,1)\)
• Model 3: \(\alpha \sim U(0,1), \quad \beta \sim Exp(1)\)
• Model 4: \(\alpha_c \sim U(0,1), \quad \beta_c \sim Exp(1)\)
• Model 5: \(\alpha \sim U(0,1), \quad \beta \sim Exp(1), \quad \alpha_c \sim U(0,1), \quad \beta_c \sim Exp(1)\)

2. 혼동 행렬(Confusion Matrix) 분석

figure 4의 (A)와 (B)는 모델 복원 실험을 수행한 후 얻어진 혼동 행렬(confusion matrix) 을 보여준다. 혼동 행렬의 각 셀은 \(p(\text{fit model} \mid \text{simulated model})\), 즉 특정 모델이 생성한 데이터를 다른 모델들이 얼마나 잘 설명하는지 확률적으로 나타낸 것이다. 읽는 방법은 simulated model (여기서 만들어진 데이터가) -> fitted model (어디서 가장 설명이 잘 되는지) 방향으로 읽으면 된다.(즉 row의 합이 1이다.) 완벽한 경우(이상적인 모델 복원)라면, 혼동 행렬은 단위 행렬(identity matrix) 이어야 한다.

이 실험에서는 소프트맥스 파라미터 \(b\) 및 \(\beta_c\) 가 작은 값도 포함되었다. \(b\) 값이 작으면, 모델의 행동이 랜덤하게 변하면서 모델 간 차이가 흐려지므로 구별이 어려워진다. 결과적으로, Model 3~5가 서로 구별되지 않으며, 혼동 행렬이 뚜렷한 대각선 형태를 띠지 않게 된다.

이 결과를 보고 \(b\) 및 \(\beta_c\) 값의 최소값을 1 이상으로 설정하면, 모델의 선택 행동이 더 결정적으로 변하는 것을 볼 수 있다. 결과적으로, 모델 간 차이가 더 명확해지며, 혼동 행렬의 대각선 성분이 더욱 뚜렷해진 것을 볼 수 있다. 이 결과를 보고 노이즈가 많으면(낮은 \(b\) 값 포함) 모델이 서로 구별되지 않지만 노이즈를 줄이면(높은 \(b\) 값 유지) 모델끼리 명확하게 구분됨을 알 수 있다. 즉, 혼동 행렬의 품질은 모델이 생성한 데이터의 파라미터 범위에 따라 달라질 수 있으므로, 실제 실험 데이터에서 얻어진 파라미터 범위와 일치시키는 것이 중요하다.

figure 4. Confusion matrices in the bandit task showing the effect of prior parameter distributions on model recovery. Numbers denote the probability that data generated with model X are best fit by model Y, thus the confusion matrix represents $$ p(\text{fit model} \mid \text{simulated model}) $$

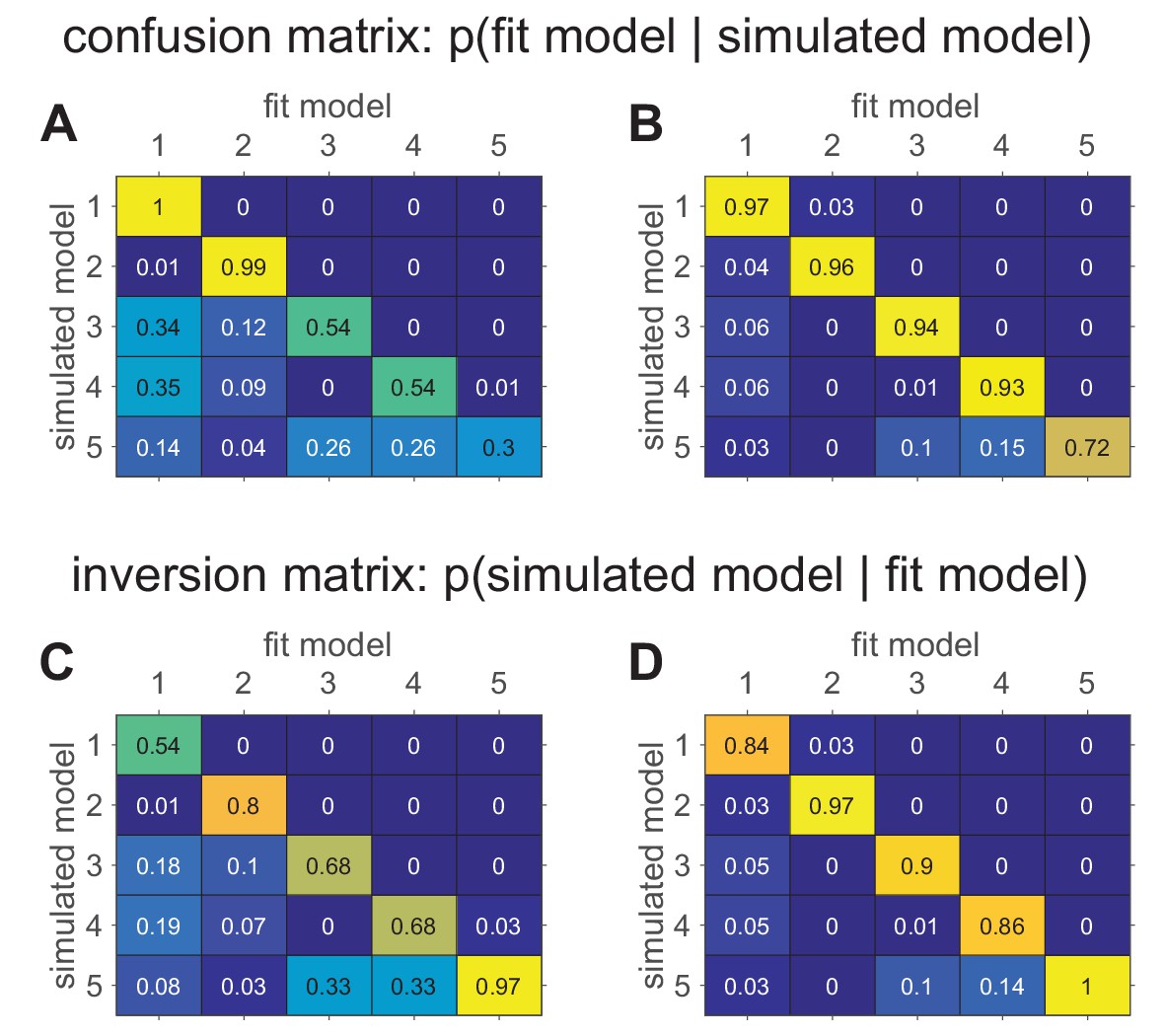
3. 역행렬(Inversion Matrix) 분석

figure 4의 (C)와 (D) 는 역행렬(Inversion Matrix) 을 보여준다. 역행렬은 \(p(\text{simulated model} \mid \text{fit model})\) 을 나타내는데, 주어진 데이터에서 특정 모델이 가장 잘 맞는다고 판단되었을 때, 실제로 어떤 모델에서 데이터가 생성되었을 가능성이 높은지를 나타낸다. 읽는 방법은 fitted model (여기와 가장 잘 맞는 데이터가) -> simulated model (어디서 만들어진 데이터 같은지) 방향으로 읽으면 된다. (즉 column의 합이 1이다.)

혼동 행렬은 모델 복원 성능을 평가하는 데 유용하지만, 실제 실험 데이터를 분석할 때, 특정 모델이 가장 잘 맞았다고 해서 반드시 그 모델이 진짜 생성 모델이라는 보장은 없다. 이 문제를 해결하기 위해, 베이즈 정리(Bayes’ Rule)를 이용해 역행렬을 계산할 수 있다. figure 4의 혼동 행렬에서, Model 1의 혼동 행렬의 대각선 값이 1.00으로, 모델 1에서 생성된 데이터는 다시 모델 1에서 가장 잘 피팅된다. 그러나, figure 4의 역행렬에서 Model 1이 데이터 생성 모델일 확률은 54%로 낮은데, 이는 Model 1이 가장 잘 맞는다고 해도, 실제 데이터가 Model 1에서 생성되었을 확률이 높지 않다는 것을 의미한다.

반면, Model 5는 혼동 행렬에서 30%만 복원되었지만, 역행렬에서는 97% 확률로 데이터가 Model 5에서 생성되었을 가능성이 높다고 분석되었으며, (D) 노이즈 감소 후에도 비슷한 패턴을 보인다.

Box 6. Example: improving parameter recovery by modeling unimportant parameters.

이 부분에서는 “중요하지 않은(unimportant) 파라미터” 를 모델에 포함시키는 것이 중요한 파라미터(예: 학습률 \(\alpha\) 및 소프트맥스 파라미터 \(\beta\))의 복원 성능을 어떻게 향상시키는지를 설명한다. 즉, 연구자가 직접적으로 관심을 두고 있는 변수(예: 학습률)를 더 정확하게 추정하기 위해, 본래 연구 질문과 관련이 없는 기저 편향(bias)과 같은 요소를 모델에 포함시킬 필요가 있을 수 있다.

1. 연구 배경 및 실험 설정

연구진은 Rescorla-Wagner 학습 모델(Model 3)에 “선택 편향(side bias)”을 추가했을 때, 파라미터 복원 성능이 향상되는지 평가하는 실험을 수행하였다. 일반적으로 Rescorla-Wagner 모델에서 선택 확률은 다음과 같이 정의된다.

\[p_{\text{left}, t} = \frac{1}{1 + \exp(\beta(Q_{\text{right}, t} - Q_{\text{left}, t}))}\]

\(Q_{\text{left}, t}\) 와 \(Q_{\text{right}, t}\) 는 각각 왼쪽과 오른쪽 선택지의 기대값(Q-values), \(\beta\) 는 소프트맥스 선택성(결정성) 파라미터로, 왼쪽과 오른쪽 선택지의 기대값 차이에 따라 선택 확률이 결정되는 방식이다. 그러나, 실험 참가자는 왼쪽이나 오른쪽 선택지를 선호하는 편향(side bias) 을 가질 수 있다. 이를 반영하여, 왼쪽 선택지의 기대값을 \(B\) 만큼 변화시키는 모델을 추가적으로 고려함.

\[p_{\text{left}, t} = \frac{1}{1 + \exp(\beta(Q_{\text{right}, t} - Q_{\text{left}, t} - B))}\]

여기서 \(B\) 는 왼쪽 선택지에 대한 편향값(side bias)을 나타내며, \(B > 0\) 이면, 오른쪽 선택지가 더 매력적으로 보이고, \(B < 0\) 이면, 왼쪽 선택지가 더 매력적으로 보이게 된다. 즉, 이 모델에서는 행동이 단순히 보상 학습(Q-learning)만으로 결정되는 것이 아니라, 선택 편향도 영향을 미친다고 가정한다.

2. 실험 방법

연구진은 위의 두 모델(기본 모델 vs. 편향 포함 모델)을 비교하기 위해 다음과 같은 실험을 수행했다. 각 참가자는 50번의 시행(trial)으로 구성된 총 10개의 독립적인 이중 선택 과제(two-armed bandit tasks)를 수행하였다.

보상 확률은 이전과 같다.

\((p_{\text{left}}, p_{\text{right}}) = (0.2, 0.8)\)
\((p_{\text{left}}, p_{\text{right}}) = (0.8, 0.2)\)

초기 \(Q\) 값은 \(Q_{\text{left}, 1} = Q_{\text{right}, 1} = 0.5\) 로 설정되었고, 두 가지 모델을 사용하여 데이터를 피팅(fitting)하고, 학습률 \(\alpha\) 및 소프트맥스 \(\beta\) 를 복원(recovery)하였다. 두 모델을 비교하여, 원래 사용된 \(\alpha\) 및 \(\beta\) 값이 얼마나 정확하게 복원되는지 figure 5에서 결과를 시각화하였다.

1. 실험 결과: 편향을 포함하면 파라미터 복원 성능 향상

figure 5. Modeling unimportant parameters provides better estimation of important parameters.

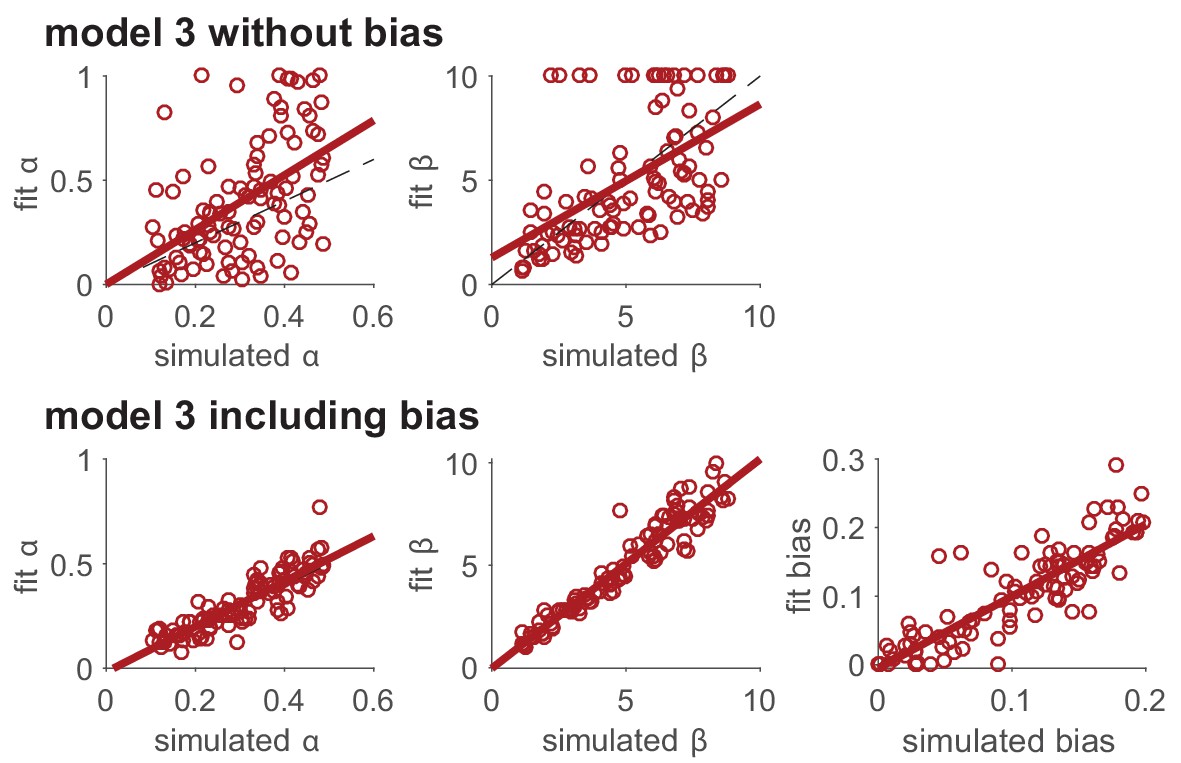
figure 5에서 보듯이, 편향 \(B\) 를 포함한 모델을 사용할 때 학습률 \(\alpha\) 와 소프트맥스 \(\beta\) 의 복원 성능이 향상되었다.

상단(기본 모델)은 편향을 고려하지 않은 상태에서 \(\alpha\) 와 \(\beta\) 를 복원하려고 하니, 데이터의 변동성이 커지는 것을 확인하였다. 결과적으로, 학습률 \(\alpha\) 와 소프트맥스 \(\beta\) 가 원래 설정된 값과 크게 다르게 복원되는 경우가 많았다. 반면 편향 \(B\) 를 모델에 추가한 후에는, \(\alpha\) 와 \(\beta\) 가 원래 설정된 값과 훨씬 더 잘 일치하는 결과가 나왔다. 이는 편향이 노이즈로 처리되지 않고 모델 내부에서 조정되므로, 학습률과 소프트맥스 값이 더 정확하게 추정되는 것으로 생각된다.

그렇다면 왜 이런 차이가 발생할까? 기본 모델에서는 편향 \(B\) 가 고려되지 않으므로, 데이터에서 편향에 의해 발생한 선택 패턴을 학습률 \(\alpha\) 또는 소프트맥스 \(\beta\) 의 변동으로 잘못 해석할 수 있다. 다시 말해 편향을 무시하면, 모델이 이를 “노이즈”로 간주하여 중요한 파라미터(\(\alpha\), \(\beta\))가 왜곡될 수 있는데, 편향을 포함하면, 노이즈가 줄어들어 중요한 학습 파라미터를 더 정확하게 추정할 수 있다는 것이다.

Box 7. Example: model validation where the fit model performs too well.

이 부분에서는 모델 검증(model validation)에서 발생할 수 있는 또 다른 오류 사례를 설명한다. 이전 포스트에서 소개한 Palminteri et al. (2017) 사례에서는 모델이 너무 못해서 실패한 경우였지만, 이번 예제(Box 7)에서는 모델이 너무 잘해서 실패하는 경우를 보여준다. 여기서의 요점은 모델이 데이터를 지나치게 잘 예측하는 경우에도, 검증 과정에서 신중하게 해석해야 한다는 점을 강조한다.

1. 실험 개요

연구진은 강화 학습을 수행하는 두 개의 에이전트(agent) 를 비교했다. 에이전트들은 자극(stimulus)에 따라 특정 행동을 선택하면 보상을 받는 과제를 수행한다. 실험 과제는 결정적 자극-행동 학습(Deterministic Stimulus-Action Learning Task)으로, 피험자는 세 가지 자극(s1, s2, s3) 을 보고, 각 자극에 대해 보상을 받을 수 있는 세 가지 행동(a1, a2, a3) 중 하나를 선택해야 한다.

조건은 다음과 같다.

• \(s_1\) → \(a_1\) 선택 시 보상
• \(s_2\) → \(a_1\) 선택 시 보상
• \(s_3\) → \(a_3\) 선택 시 보상
• \(a_2\) 는 어떤 자극에서도 보상을 받을 수 없음.

즉, 참가자는 주어진 자극(s)에 따라 보상을 받기 위해 적절한 행동(a)을 학습해야 한다.

2. 비교한 두 가지 강화 학습 모델

1. 블라인드 에이전트(Blind Agent)

자극(s)을 고려하지 않고 행동(a)에 대한 가치 \(Q(a)\) 만 학습하는 모델로, 특정 자극에서 어떤 행동이 가장 좋은지를 학습하는 것이 아니라, 전반적으로 어떤 행동이 좋은지를 학습한다. 이를 수식적으로 표현하면:

\[Q(a_i) = Q(a_i) + \alpha \cdot (r - Q(a_i))\]

• \(Q(a_i)\) : 행동 \(a_i\) 의 기대 보상 값
• \(\alpha\) : 학습률(learning rate)
• \(r\) : 받은 보상

이 모델은 단순한 행동-가치 기반 학습(Value-based learning) 모델로 자극(s)의 영향을 고려하지 않고, 행동 자체의 보상만을 학습한다.

2. 상태 기반 에이전트(State-Based Agent)

자극(s)과 행동(a)의 조합 \(Q(a, s)\) 을 학습하는 모델로, 각 자극마다 행동에 대한 별도의 보상 기대치를 학습한다. 이를 수식적으로 표현하면:

\[Q(a_i, s_j) = Q(a_i, s_j) + \alpha \cdot (r - Q(a_i, s_j))\]

• \(Q(a_i, s_j)\) : 자극 \(s_j\) 에서 행동 \(a_i\) 의 기대 보상 값
• \(\alpha\) : 학습률(learning rate)
• \(r\) : 받은 보상

이 모델은 각 자극마다 보상을 다르게 학습할 수 있고, 자극이 다를 경우 같은 행동을 선택하더라도 다른 결과를 학습할 수 있다.

3. 실험 결과

연구진은 두 모델을 이용해 데이터를 생성한 후, 두 모델을 각각 피팅하여 비교했다.

블라인드 에이전트와 상태 기반 에이전트의 학습 곡선을 비교했을 때, 모델 파라미터를 적절히 조정하면, 두 모델의 학습 곡선이 매우 유사해질 수 있었다. 즉 눈으로 보았을 때 두 모델은 비슷한 방식으로 학습하는 것처럼 보였다.

연구진은 상태 기반 모델(state-based model)이 두 에이전트(블라인드 vs. 상태 기반)의 행동을 얼마나 잘 예측하는지 평가했다.(figure 6B) 놀랍게도, 상태 기반 모델이 블라인드 에이전트의 행동을 더 높은 확률로 예측하는 결과가 나타났다. 블라인드 에이전트의 행동을 예측하는 정확도가 원래 상태 기반 모델의 행동을 예측하는 정확도보다 더 높았는데 이는 직관적으로 이해하기 어려운 결과이다.

figure 6. An example of successful and unsuccessful model validation. (A) Behavior is simulated by one of two reinforcement learning models (a blind agent and a state-based agent) performing the same learning task. Generative parameters of the two models were set so that the learning curves of the models were approximately equal.

연구진은 이 결과가 노이즈(softmax 파라미터)의 차이 때문이라는 것을 발견했다. 블라인드 에이전트는 결정적(deterministic) 행동을 보이며, 노이즈가 낮은 반면 상태 기반 에이전트는 더 높은 노이즈를 가지며, 선택 행동이 불확실하다. 따라서, 상태 기반 모델은 블라인드 에이전트의 행동을 상대적으로 쉽게 예측할 수 있었던 반면, 상태 기반 에이전트 자신의 행동은 더 어렵게 예측되었다.

연구진은 상태 기반 모델을 피팅한 후, 피팅된 파라미터를 이용해 새로운 학습 곡선을 생성했다.(figure 6C) 상태 기반 모델을 원래 상태 기반 에이전트에 피팅하면, 유사한 학습 곡선이 생성지만 블라인드 에이전트에 피팅한 후 생성된 학습 곡선은 너무 잘 학습하는 경향을 보였다. 즉, 모델 검증을 수행해보니 상태 기반 모델은 블라인드 에이전트의 행동을 지나치게 잘 예측하고 있었음이 드러났다.